How smooth is your ride? Comparison of sensors and methods for surface quality assessment using IMUs

Moritz Beeking; Hannah Wies; Markus Steinmaßl; Karl Rehrl

doi:10.55329/guai2275

Introduction

Faced with climate change, congestion and health issues, governments and public bodies throughout the world should try (EC, 2023; Holger et al., 2015; UN, 2024) to promote cycling as a sustainable, space efficient, and healthy mode of transport. An important factor for people's decision to ride a bicycle is cycling comfort (Ayachi et al., 2014; CROW, 2016). The surface roughness of bicycle infrastructure is, among others, a vital component of bicycle comfort (Castañon & Ribeiro, 2021; Hoelzel et al., 2012; Landis et al., 1997). Multiple works also mention roughness to influence safety (Hoelzel et al., 2012; Kranzinger & Leitinger, 2021; Zang et al., 2018) or actively investigate the correlation (Astarita et al., 2014; Gadsby et al., 2022). Furthermore, well-established methods to measure surface roughness exist. Most works on measuring the surface roughness of bicycle infrastructure use acceleration data collected with IMUs (Bíl et al., 2015; Kranzinger & Leitinger, 2021; Litzenberger et al., 2018; Nuñez et al., 2020; Zang et al., 2018). The collected accelerations are then further processed on a segment-wise basis to derive roughness metrics. However, there are different approaches to every single step of this process. With the details explained in section 2, there are differences in the type of IMU used, mounting position, sampling frequency, segment length and used axes of the accelerometer.

The most important well-defined standard in the context of surface roughness measurement is ISO 2631-1 on ‘Mechanical vibration and shock - Evaluation of human exposure to whole-body vibration’. It defines acceptable vibrational acceleration levels measured an weighted at different frequencies between 0.1 Hz to 80 Hz. Measurement locations, directions, and further process characteristics are also lined out. (ISO, 1997)

Furthermore, the International Roughness Index (IRI) is a well-established metric in road surface assessment. It is defined as the vertical displacement between the actual road surface and a virtual ideal plane. Its unit is either millimeters of displacement per traveled meter or meters of displacement per traveled kilometer (metric system, identical), or inches of displacement per mile traveled (imperial system, linearly proportional). The IRI is based on the so-called quarter-car model simplifying vehicles to a single wheel with both sprung and unsprung mass atop. (Sayers & Karamihas, 1998)

Although based on ISO 2631-1 and the IRI some recurring aspects exist, every work introduces its own method of calculating roughness based on the measured accelerations. While the findings of some of these works have been cursorily compared (Gadsby & Watkins, 2020), a proper comparison of methods and their characteristics has not been conducted yet. Similarly, according to a recent review on the related topic of bikeability indices (Castañon & Ribeiro, 2021), several existing works point out that the lack of comparability and standardization is hampering the applicability of bikeability indices. The same effect can be assumed for surface roughness indices. Therefore, the aim of this work is to compare the results of applying selected roughness calculation methods to data collected with two different sensors during the same test rides. The overall process to do so is outlined in Figure 1.

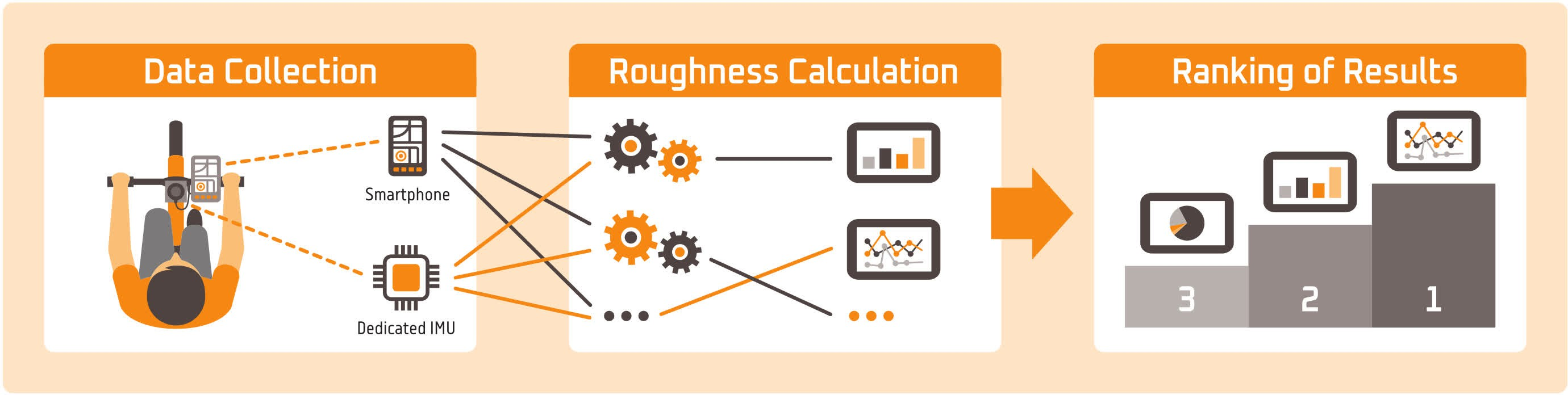
https://typeset-prod-media-server.s3.amazonaws.com/article_uploads/9098b204-d7db-48a4-98be-95290089f3fc/image/ebf82380-97d5-411b-9734-4ca3dd25c51b-ufigure_1.png — **Figure 1: Comparison process outline**

As described in detail in section 3, two criteria were developed for comparison of the resulting assessments. First, the reliability, defined as the agreement of any given assessment with all other assessments for the same segment. And second, the stability, defined as the inverse of the dispersion of each sensor-method combination per segment. Based on these criteria, each sensor-method combination's assessments are evaluated. Finally, using these evaluations as well as practical considerations like sensor availability or ease of method implementation, recommendations for choosing the right sensor-method combination for a given task are provided.

The rest of this work is structured as follows. First, the most relevant works on bicycle comfort and especially roughness assessment based on acceleration measurements are described. Special attention is given to the selection of the five works chosen for comparison. Subsequently, the methodology consisting of data collection, roughness calculation and comparison of results is described in detail. Next, the stability and reliability of the different sensor-method combinations are compared and interesting findings pointed out. Last, the work is concluded by emphasizing the main findings and their implications for bicycle infrastructure assessment, and finally pointing out possible future research directions.

Related work

The research fields of cycling comfort estimation and especially surface roughness estimation based on acceleration measurements have both been well explored in the past. The following chapter will first outline some relevant reviews and works on bicycle comfort, emphasizing the role of surface roughness. Subsequently, typical sensor setups and measuring parameters for acceleration measurement are presented. Next, the basics of roughness calculation and some notable examples are presented. Finally, the selection process used to decide which methods to feature in this comparison, as well as some general features of the selected methods will be described. The in-depth explanation of the implemented methods can be found in section 3.

Cycling comfort and surface roughness

Numerous concurring definitions of cycling comfort can be found in literature (CROW, 2016; Castañon & Ribeiro, 2021; Landis et al., 1997; Yamanaka & Namerikawa, 2007; Yamanaka et al., 2013). However, there are certain recurring aspects of comfort mentioned by the majority of works on the topic. Both cycling comfort in general and its sub-aspect surface roughness are often referred to in so called bikeability indices trying to assess how well-suited a given area is for cycling. The review of bikeability indices by Castañon and Ribeiro (2021) provides a good overview of recent works on the topic and, more relevant here, bikeability criteria considered by these works. The criteria analyzed most often are geometric design features of the cycling infrastructure, the accessibility of relevant areas, the traffic safety and the topography of the study area. Each of these aspects was considered by eight out of the 14 works they looked at. The geometric design features include the surface type and condition, used by 5 out of the 14 works as a bikeability indicator. The only other indicator also used by five of the included works was the presence of dedicated cycling infrastructure. Thus, the surface roughness, considered to result from the combination of surface type and condition, can be considered to be among the most relevant aspects of cycling comfort. (Castañon & Ribeiro, 2021)

https://s3-us-west-2.amazonaws.com/typeset-prod-media-server/bfe17e6a-d489-4c14-86ba-f40207139430image2.png — Figure 2: Common mounting positions of accelerometers for surface roughness assessment.To the top right of either drawing, the corresponding axes are annotated. These are the assumed axes of the bicycle, the axes of the actual accelerometers should be expected to be at least slightly rotated.

Yamanaka et al. (2013) and Yamanaka and Namerikawa (2007) developed and calculated a bicycle level-of-service in two separate works. In the first work (Yamanaka & Namerikawa, 2007), they listed the roughness of the road surface, the required effort by the cyclist, and braking, slow speed, speed deviation and comfort of speed as the main factors of a bicycle level-of-service. For the second work (Yamanaka et al., 2013), they changed this list to the stability of the speed, stops, vibrations, steering, traffic density, and braking behavior. Although in the later work vibrations were considered less important, they still confirm surface roughness to be a relevant aspect of cycling comfort.

Surface roughness being of major importance to cycling comfort is not a new concept either. In the late eighties, Axhausen et al. already found it to be of importance especially for experienced cyclists in a preference study (Axhausen & Smith, 1986). This was later experimentally proven by Landis et al., finding a strong correlation between pavement surface condition and participants comfort perception (Landis et al., 1997). Last, the English version of the Dutch CROW Design Manual for Bicycle infrastructure, often considered a kind of gold standard for cycling infrastructure, states ‘The surfacing on the road section should satisfy the requirements in terms of evenness.’ (CROW, 2016).

Acceleration measurements

Measuring surface roughness of cycling infrastructure based on accelerations is a well established approach with recurring components found in literature. While several, especially earlier, works used dedicated accelerometers (Bíl et al., 2015; Gao et al., 2018; Neto et al., 2018; Olieman et al., 2012), most recent works rely on smartphones for data collection (Kranzinger & Leitinger, 2021; Litzenberger et al., 2018; Nuñez et al., 2020; Wijerathne et al., 2018; Zang et al., 2018). In most cases, authors use vertical acceleration values, either by installing the IMU in such a way that one axis is perpendicular to the ground plane (Bíl et al., 2015; Nuñez et al., 2020), or by calculating the resulting vertical acceleration from all three axes (Kranzinger & Leitinger, 2021; Neto et al., 2018; Zang et al., 2018). Some works use all three axes of the accelerometer directly (Gao et al., 2018; Litzenberger et al., 2018). The accelerometers and smartphones in these studies are mounted to the fork (Bíl et al., 2015), the handlebar stem (Kranzinger & Leitinger, 2021; Zang et al., 2018), the left or right half of the handlebar (Gao et al., 2018), or the front (Litzenberger et al., 2018; Neto et al., 2018) or back (Nuñez et al., 2020) of the top tube. Typical sampling frequencies for the acceleration data range between 20 Hz (Bíl et al., 2015) and 100 Hz (Litzenberger et al., 2018; Zang et al., 2018), with 50 Hz being most common (Harikrishnan & Gopi, 2017; Kranzinger & Leitinger, 2021; Neto et al., 2018; Nuñez et al., 2020; Wijerathne et al., 2018) and occasional higher values up to 512 Hz (Calvey et al., 2015).

Roughness calculation

With regard to the roughness calculation, ISO 2631-1 (ISO, 1997) on whole body vibrations is often mentioned as a basis for roughness measures and indices (Gao et al., 2018; Nuñez et al., 2020). Furthermore, the IRI (Sayers & Karamihas, 1998) is a well-established roughness measure. Therefore, some works try to directly calculate it (Zang et al., 2018), while some consider closely related measures (Bíl et al., 2015; Gao et al., 2018). Other works introduce their own comfort measures not related to ISO 2631-1 or the IRI (Kranzinger & Leitinger, 2021; Wijerathne et al., 2018).

Roughness calculation is typically performed on a segment-wise basis. There is no standard segment length, with 5 m (Nuñez et al., 2020), 10 m (Kranzinger & Leitinger, 2021), 20 m (Zang et al., 2018), and 100 m (Bíl et al., 2015) all found in literature. In some works, test rides are not segmented further and instead roughness is calculated per test route. Gao et al. (2018) analyzed test routes with an average length of 250 m, while (Litzenberger et al., 2018) choose test routes with approximately 100 m each. Neto et al. (2018) did not group the measured accelerations by travel distance but by time, calculating roughness for every 2 seconds of collected data.

In recent years, sensor equipped bicycles have become a lot more prevalent than before, also yielding more works on surface roughness assessment. A very good overview of the use of these sensor bicycles in research was compiled by (Gadsby & Watkins, 2020). They list six works investigating pavement condition. Two works by the same research group (Calvey et al., 2015; Taylor & Fairfield, 2010) describe a sensor bike suited for acceleration measurement but no actual calculation of surface roughness. One work used a neural network to classify different pavements (Neto et al., 2018), however their description was considered unsuited for reimplementation. Two works (Bíl et al., 2015; Nuñez et al., 2020) were chosen for comparison and are described in the next section.

Wijerathne et al. (2018) describe a sophisticated approach to calculate surface roughness independent of accelerometer position and orientation. To this end, they used four smartphones, one mounted on the handlebar, one in a front bag, one attached to the test riders arm, and one carried in a backpack. They used a wavelet-transform followed by a Taylor expansion and tested for Lipschitz continuity to detect bumps. Although impressive, their work was not chosen for comparison in this work. The reason is their focus on detecting single bumps, making comparison with methods yielding a segment-wise roughness metric difficult (Wijerathne et al., 2018).

Used methods

From the numerous works using IMUs on bicycles for surface roughness calculation, a selection was made based on three considerations:

Popularity: well-cited works were chosen over less known ones in an attempt to compare the most used and therefore most relevant approaches.
Quality of description: for comparison, a reimplementation of the selected methods was necessary. Therefore, methods were excluded if their original description was not sufficiently detailed for this.
Uniqueness: methods significantly different from others were chosen over slight alterations of more popular works.

Ultimately, five works were chosen for comparison. The works by Bíl et al. (2015) and Zang et al. (2018) are the most cited works on roughness calculation from accelerations measured using a sensor-equipped bicycle. Bíl et al. (2015) describe their algorithm for roughness calculation commendably concise. Zang et al. (2018) on the other hand are among the few authors using more than one accelerometer axis for their calculations. However, as a first step they derive the vertical acceleration for further processing. Gao et al. (2018) are among the even fewer authors actually using all axes and their work is still fairly popular. All of these methods produce numerical metrics. However, for further use in categorization or maintenance of bicycle infrastructure, ordinal metrics are often preferable. Therefore, two works presenting methods yielding such metrics were also chosen for comparison: The work by Nuñez et al. (2020) combines video analysis and acceleration measurements for assessing the quality of cycling infrastructure. To this end, they also present an adaption of the ISO 2631-1 (ISO, 1997), yielding six comfort classes for surface roughness. Last, the method presented by Kranzinger and Leitinger (2021) has been chosen for comparison. It also yields an ordinal metric for surface roughness and, more interestingly, is not based on the acceleration itself but its first derivative, the so called jerks. The methods for roughness calculation from accelerations used in these works are described in detail in section 3, together with descriptions of the corresponding reimplementations. The remainder of this chapter outlines the general approach of each of these works, especially aspects not found in other works.

Bíl et al. (2015) measure accelerations using a relatively low frequency of 20 Hz, compared to the 50Hz found in most works. The accelerometer is attached to the fork of the bicycle in such a way that one axis is considered vertical and used for roughness calculation. The separate GNSS sensor is mounted to the handlebar, both signals are combined after collection based on their timestamps. For roughness calculation, only downwards accelerations >1 g are used. The resulting so-called dynamic comfort index (DCI) ranges between zero and one. Higher values correspond to more comfortable roads. (Bíl et al., 2015)

The work by Zang et al. (2018) is based on the idea of the quarter-car model used for calculation of the IRI (Sayers & Karamihas, 1998). They measure accelerations at 100 Hz and GNSS localizations at 1 Hz using a smartphone mounted to the handlebar stem. Vertical acceleration is derived by projection of measured accelerations with a reference unit vector calculated from stand still points at the beginning of each test run. The IRI is meant to represent vertical displacement. In order to calculate it, double integration of the vertical accelerations is used. The resulting IRI is measured in mm/m vertical displacement and ranges from zero to approximately 12 mm/m on their test tracks. (Zang et al., 2018)

Gao et al. (2018) used an accelerometer mounted on the left half of the handlebar and a separate GNSS sensor for data collection. They report neither acceleration nor GNSS recording frequency. Their test subject was instructed to keep a constant speed between 12 km/h to 16 km/h. Following ISO 2631-1 (ISO, 1997), they weighted the measured accelerations in the frequency domain using a small band filter. Unfortunately, they do not report on the parameters of the weighting or the filter. Notably, they use all three axes of the accelerometer for roughness calculation without extracting the vertical component first. Their so called Dynamic Cycling Comfort (DCC) ranges between zero and just above three for their test routes. (Gao et al., 2018)

Nuñez et al. (2020) use two sensors to calculate their so called Bicycle Environment Quality Index (BEQI), a camera mounted at the front of the frame for capturing videos and a smartphone mounted on the top tube in front of the saddle to capture accelerations. The smartphone is mounted parallel to the ground such that a single accelerometer axis is considered the vertical acceleration. Accelerations are sampled at 50 Hz. Notably, they used frequency analysis to find characteristic frequencies of different pavement types. Based on ISO 2631-1 (ISO, 1997), roughness is rated as one of six classes depending on the root mean square of vertical accelerations. (Nuñez et al., 2020)

Kranzinger and Leitinger (2021) are the only authors using the derivative of vertical accelerations, called jerks, to calculate surface roughness. They assessed the surface roughness of impressive 436.6 km of cycling infrastructure, analyzing 5 166 km of test runs. Accelerations are captured using a smartphone mounted to the stem of the handlebar. Accelerations are sampled at 50 Hz and GNSS localizations at 1 Hz. Subsequently, four roughness classes are calculated per 10 m segment using the k-means++ clustering algorithm (Arthur & Vassilvitskii, 2007). As input parameters, the average jerk value and the share of jerks above a given threshold of 1 200 m/s³ are used. The roughness metric of each section is then defined as the class it is assigned to by the clustering. (Kranzinger & Leitinger, 2021)

Methodology

The presented work consists of three main steps described in detail in the remainder of this chapter: data collection, roughness calculation and comparison of results. For data collection, methods from different existing works are combined in an attempt to facilitate broad applicability of our results. Roughness calculation is carried out using careful reimplementations of preexisting algorithms. The methods for result comparison were specifically developed for this work based on well-established statistical metrics. The general flow of data, as displayed in Figure 1, is as follows:

Data is collected by a smartphone and a dedicated IMU/GNSS simultaneously.
The data is fed into multiple methods from literature calculating metrics intended to represent the surface roughness.
The resulting assessments are sent to evaluation algorithms calculating stability and reliability metrics for each sensor-method-segment-length combination.

Data collection

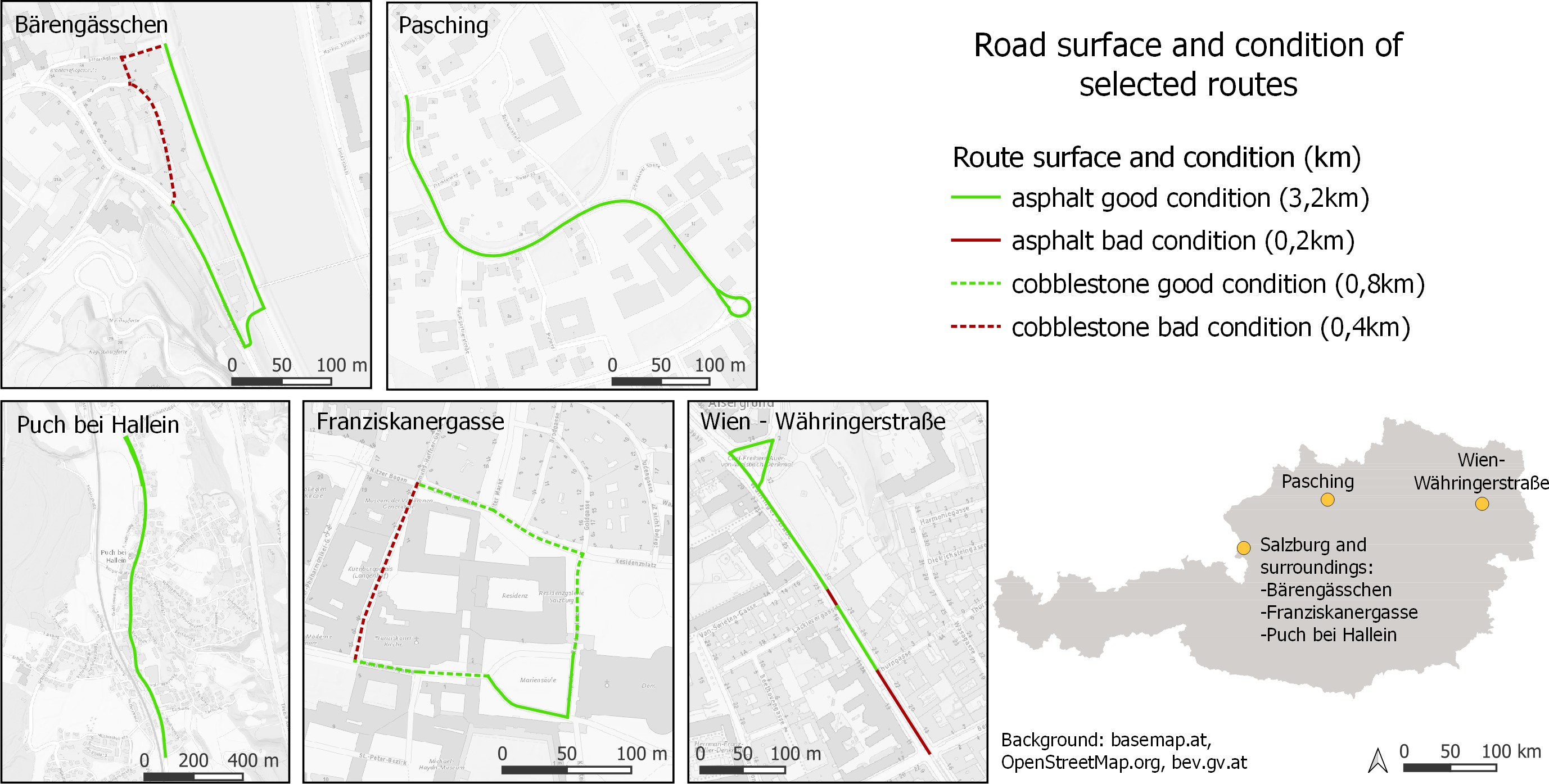
The data used in this work was collected between September and November 2023 in four cities and villages in Austria. The test routes are depicted in Figure 3. Each route was driven 8–16 times. A smartphone and a dedicated IMU-GNSS-device were mounted side by side for simultaneous data collection. For each route, data was collected in one continuous session, without remounting of any sensors, as to keep their position and orientation steady. The collected data was matched to the so called ‘Graphenintegrationsplattform’ (GIP), a national Austrian digital road graph (Neto et al., 2018; ÖVDAT, 2022). The generated trajectories were split into segments of differing length for segment-wise roughness calculation. Data from both sensors was brought to a common data format and collected in a single data set for further processing.

https://typeset-prod-media-server.s3.amazonaws.com/article_uploads/9098b204-d7db-48a4-98be-95290089f3fc/image/cc0de139-1bdb-49b6-a0bc-a3d11e6156a8-ufigure_3.png — **Figure 3: Test routes investigated in this work. Note the different scales per map, which are a consequence of the very different lenghts of test routes.**

Sensor setup

The sensor setup used for this work is depicted in Figure 4. It consists of two different sensors in different mounting positions. As discussed in section 2, most recent works rely on smartphones for acceleration measurement. The reasons are their ubiquitous availability and ease of combined acceleration-localization data collection. However, to the best of the authors' knowledge, no comparison whether a dedicated, industrial grade IMU would yield more reliable or stable assessments has been undertaken yet.

https://typeset-prod-media-server.s3.amazonaws.com/article_uploads/9098b204-d7db-48a4-98be-95290089f3fc/image/02d8ebd7-370c-4239-8300-d53b5d59d458-ufigure_4.png — Figure 4: Sensor setup for acceleration data collection. The Xiaomi Mi 9X smartphone can be seen attached to the right half of the handlebar. The round dark grey device on the handlebar stem is the XSens MTI-680G, containing an industrial grade IMU and GNSS sensor. As can be seen, the XSens is slightly tilted upwards, yielding an IMU z-axis slightly pointing backwards towards the rider. The Smartphone on the other hand is tilted back and to the left, resulting in an IMU z-axis pointing approximately towards the riders left shoulder.

The two most popular mounting positions found in literature are the handlebar stem and the top tubes' front end. These are very close to each other, however, like the sides of the handlebar, the handlebar stem turns when steering while the top tube does not. The handlebar right and left of the stem is not often used in literature. However, it is also a commonly used mounting position for smartphones used for navigation and similar tasks. These considerations yielded the following sensor setup:

An XSens MTI-680G1¹ containing both an industrial-grade IMU and GNSS sensor mounted to the stem of the handlebar.
A Xiaomi Mi 9X smartphone mounted in the right half of the handlebar using a rigid steel mounting kit.

Map matching

To calculate roughness of specific road segments, the collected data is first mapped onto a graph representation of the underlying road network. The GIP, a national Austrian digital road graph (ÖVDAT, 2022) was chosen for this. The GIP divides roads into sections delimited by points were another road is met or a significant road characteristic, like the number of lanes, changes. Especially in inner city scenarios, this may yield many very short sections.

Roughness calculation is usually done for fixed length segments. For this work, the selected legths are: 5 m (Nuñez et al., 2020), 10 m (Kranzinger & Leitinger, 2021), 20 m (Zang et al., 2018), and 100 m (Bíl et al., 2015). Gao et al. (2018) did not use fixed length segments but defined test routes with an average length of 250 m. To calculate the segment-wise roughness assessments, the mapped data points are regrouped by specifically created fixed-length segments. This is done by subdividing GIP sections into segments of the given length and combining parts of them where necessary. To map the collected data onto the GIP, the following steps are performed:

First, for each test run, a trajectory consisting of all collected GNSS localizations and their correspond- ing time stamps is extracted.
These are mapped onto the GIP sections using an existing implementation of the approach described by (Rehrl et al., 2018).
For each route, the segmentation into fixed length segments is calculated such that any given position on any GIP section along the test route corresponds to exactly one fixed-length segment.
The section-mapped accelerations are then assigned to the corresponding fixed length segments, yielding a list of measurements per test run and segment.

Data set

The data used for this study was collected along the test routes depicted in Figure 3. Test riders were instructed to keep a speed of approximately 20 km/h. In total, 72.2 km of test rides were conducted, resulting in 11.3 h of test data covering 4.6 km of cycling infrastructure with different surface types as listed in the figure. Along these routes, 77 118 GNSS localizations and 1.66 million acceleration measurements were collected. 2 691 acceleration measurements are considered to be collected from an unmoving bicycle and used for the calculation of reference vectors for the extraction of the vertical acceleration component as described in section 3.2.1. After filtering by speed as described in section 3.2.2, 834 thousand acceleration measurements, about half of the collected measurements, remained for roughness calculation. Depending on segment length, these were assigned to one of 1 193 segments of 5 m, 595 segments of 10 m, 296 segments of 20 m, or 57 segments of 100 m length. The apparent mismatch with the reported 4.6 km of infrastructure is a consequence of segments driven in both directions being counted once for total assessed infrastructure but twice (once per direction) when creating fixed length segments. The slight mismatch between the different segment lengths is a consequence of the last parts of each test route shorter than the given length being dropped.

Roughness calculation

To calculate the roughness based on the accelerations grouped by segments there are some preprocessing steps followed by the actual roughness calculation methods. First, required for all compared methods but the one by Gao et al. (2018), the vertical component needs to be extracted from the three accelerometer axes. Also accelerations are filtered based on speed to clip stop points, slow sections and also GNSS errors resulting in very high speeds and possibly erroneously map matched measurements. Finally, the actual roughness calculation using the reimplementations of the methods selected for comparison is performed. The result is one rating per test segment, sensor and method to be compared subsequently.

Calculation of vertical acceleration component

All tested methods except the one proposed by Gao et al. (2018) use only the vertical acceleration for roughness calculation. As the two sensors were mounted in different orientations, both with no accelerometer axis pointing precisely downwards, vertical accelerations had to be calculated from all three axes. Following Zang et al. (2018), this was done using reference gravitational acceleration vectors collected while the bicycle was standing still. While the authors of Zang et al. (2018) instructed their test riders to keep the bike steady for the first five seconds of each test ride we chose a different approach. We filtered all collected accelerations by two criteria:

A speed below 10⁻ ³ m/s. This was considered as the bicycle not moving along the test route. The speed was calculated from GNSS data, GNSS sampling at 10 Hz with the localization precision limited by the used GNSS sensors. Given these prerequisites, no lower speeds were observed in the data or, upon further investigation, technically possible.
A change in resulting acceleration, i.e. the length of the resulting acceleration vector, of less than 0.1 m/s³. This prerequisite was chosen to filter out two possible situations: First, the bike not moving along the test route, but lateral rolling, like tilting sideways, or otherwise being slightly moved by mounting, operating the sensors or similar situations. And second, erroneously repeated GNSS localization yielding a speed of zero mid-ride.

The remaining accelerations were grouped by test route and sensor. The filtering by test route was done to account for possible changes in exact mount configurations between the data collected at different times. For each sensor-route pair, a reference vector $\vec{r} = (\bar{x}, \bar{y}, \bar{z})$ was chosen by taking the median of the remaining values in x, y and z direction of the accelerometer. The median was chosen to dampen the effect of possibly missed outliers. Subsequently, following Zang et al. (2018), the vertical component $a_{v}$ of each measured acceleration $\vec{a} = (x_{i}, y_{i}, z_{i},)$ was derived by projection onto the unit vector in vertical direction using Equation 1.

1

a_{v} (\vec{a}) = \frac{x_{i} * \bar{x} + y_{i} * \bar{y} + z_{i} * \bar{z}}{\sqrt{{\bar{x}}^{2} + {\bar{y}}^{2} + {\bar{z}}^{2}}}

Filtering and smoothing of speeds

With the vertical acceleration calculated for each measurements, the collected data points were filtered based on their speed. First, any measurements with calculated speeds above 40 km/h were discarded. The remaining speeds were smoothed using a rolling cosine window with a width of five measurements in order to dampen the effect of slight GNSS localization errors. Next, measurements with smoothed speeds below 15 km/h were discarded. Finally, measurements with a change in resulting acceleration since the last measurement above 5 000 m/s³ were removed, as they are also most likely erroneous. On the one hand, this removes the stops at the beginning and end of each test ride as well as stops at traffic lights and similar. On the other hand, measurements collected at speeds below this threshold are undesirable as speed has a major impact on the measured vertical accelerations. At higher speeds, identical vertical displacements yield higher accelerations as the bike is subjected to them in a shorter period of time (Gao et al., 2018; Olieman et al., 2012). Thus measurements should be collected at a constant speed.

Methods

As justified in section 2, five works and their respective roughness calculation methods were chosen for comparison. In section 2, the general approach of each of these works were outlined. In this section, their roughness calculation methods are described in detail, with an additional focus on the reimplementations used for this work.

Bíl et al. (2015) calculate their DCI according to Equation 2. $a_{v}$ represents the vertical acceleration. n represents the number of vertical accelerations greater than 1 g in one second. They grouped the accelerations by seconds as this was the sampling frequency of their GNSS sensor, allowing them to calculate one DCI value per GNSS point. As we are only interested in calculating metrics per segment, we grouped the accelerations by segments instead, with n consequently being the number of accelerations greater than 1 g per segment. The $a_{v i}$ are therefore exactly these accelerations. The gravitational acceleration of the earth is not the same around the globe. Several standard approximations of 1 g exist, with 9.81 m/s² often used for manual calculations and 9.80665 m/s² often used in engineering. However, as we calculated separate gravitational reference vectors per route-sensor pair anyways, we used the length of these as values for 1 g. Thanks to their concise description of the roughness calculation, we are confident in our reimplementation of their method.

2

D C I = {(\frac{1}{n} \sum_{i = 1}^{n} a_{v i}^{2})}^{- 1}

Zang et al. (2018) use double integration of the absolute value of the vertical acceleration $a_{v}$ divided by the traveled distance S to calculate the vertical displacement according to Equation 3. To this end, t_start and t_stop are defined as the first and last timestamp of measurements belonging to a given test segment, in the original work of 20 m length. They consider their assessment to closely reflect the IRI (Sayers & Karamihas, 1998), defined as the vertical displacement, typically measured in mm/m. Zang et al. (2018) point out, that distance calculation from speeds and timestamps might be more precise than from localizations. However, as we did not undertake any direct speed measurements, we used the fixed segment length for S. They do not report the integration approximation they used for the discrete acceleration values. We decided to use cumulative trapezoid integration for the inner integral and Simpson's rule for the outer integral. This combination was chosen as it yielded the highest agreement with the other methods and was therefore considered the best possible variant of their described method. With the travel distance calculation done differently and the assumptions on integration, it is difficult to tell how close our results are to ones achieved using their complete system. However, we remain confident that the general concept is reproduced well by our reimplementation.

3

I R I = \frac{\int \int_{t_{s t a r t}}^{t_{s t o p}} |a_{v}| {(d t)}^{2}}{S}

Of the methods compared in this work, the approach by Gao et al. (2018) is the only one taking all accelerometer axes into account beyond extracting vertical acceleration. Their approach is based on ISO 2631-1 (ISO, 1997), therefore they report to weight the accelerations in the frequency domain. Unfortunately, they do not report the corresponding weighting parameters. Therefore, this work uses unweighted accelerations for the reimplementation. It may be discussed, whether this still allows for comparability of the method, however the information Gao et al. provided did not allow for a more detailed reimplementation. For each accelerometer axis,Gao et al. (2018) calculate the root mean square value (Equation 4). Subsequently, the euclidean norm of the 3D vector consisting of these root mean square values per axis a_i is calculated for the resulting acceleration value Equation 5. This equates to calculating the resulting vector from three root mean square average vectors along the accelerometer axes and is actually the approach recommended by ISO 2631-1.

Table 1: Expected perception depending on the vertical accelerations root mean square per segment as reported by Nuñez et al. (2020)

RMS in m/s²	< 0.315	0.315 – 0.63	0.63 – 1	1 – 1.6	1.6 – 2.5	> 2.5
Expected perception	Not uncomfortable	A little uncomfortable	Fairly uncomfortable	Uncomfortable	Very uncomfortable	Extremely uncomfortable

4

a_{i} = \sqrt{\frac{1}{T} \sum_{t = 0}^{t = T} a_{i}^{2} (t)} i \in x, y, z

5

a_{v} = \sqrt{a_{x}^{2} + a_{y}^{2} + a_{z}^{2}}

Nuñez et al. (2020) use a straightforward root mean square (RMS) of vertical acceleration $a_{v}$ as can be seen in Equation 6. They report calculating this RMS per 5 m section. This work uses the same approach only testing different segment lengths. Notably, Nuñez et al. (2020) do not consider this RMS the final assessment but based on ISO 2631-1 (ISO, 1997) they define six vibrations classes as listed in Table 1. For their BEQI, they take additional factors like traffic density, bicycle parking or accessibility into account. However, as this work is focused on surface quality assessment only the RMS-based roughness rank is used for comparison.

6

R M S = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} a_{v i}^{2}}

Kranzinger and Leitinger (2021) are the only authors not working directly with the accelerations but their first order derivative, the so-called jerks. Furthermore, unlike the works by Bíl et al. (2015), Gao et al. (2018) and Nuñez et al. (2020), they do not use any variant of the root mean square of the derived values. Instead, they first calculate two parameters for each section:

The average jerk value per segment, measured in m/s³.
The share of heavy jerks per segment. In their original work they considered a ‘heavy jerk’ any jerk above 1 200 m/s³. As this value is highly dependent on the used bicycle, IMU, tire pressure, mounting position and solution, and so on, it is not used in this work. Instead a new threshold is defined, using the 70^th-percentile of jerk values per sensor. The 70^th-percentile was chosen with the clustering in mind. As it yielded a wide spread of heavy jerk shares, a truly two-dimensional clustering was possible.

The resulting average jerk value and heavy jerk share per section are then used as input to a k-means++ clustering algorithm (Arthur & Vassilvitskii, 2007). The number of clusters is fixed to four, and 20 runs with differing cluster center initializations are performed. The best resulting cluster centers are kept for later clustering. Apart from the changed heavy jerk threshold, we consider this implementation a very close reimplementation of the described method.

Comparison of results

The stated goal of this work as outlined in section 1 is to compare different sensor-method combinations and segment lengths used for surface roughness estimation. To this end, mathematically sound comparison methods are required. While numerical assessments are fairly easy to compare assuming that the assessments are normalized first, the mixture of numerical and ordinal assessment scales proved difficult to compare. For stability, no possibility of comparing numerical and ordinal assessment methods directly was found. Comparing the numerical assessments to each other was straightforward using the coefficient of variation. Comparing ordinal assessments is difficult, as one must not make the mistake of considering classes equally spaced. However, a suited measure for ordinal dispersion was found that allows for comparison of stability between ordinal methods and their combination with different sensors and segment lengths. Regarding the reliability, defined as the agreement of any given method with an ensemble of all considered methods, rank correlation was used to be able to compare all used methods to each other.

Stability calculation

The stability of assessments using a certain sensor-method combination is a metric whether applying this combination to the same test route multiple times will yield the same or differing results. This is of interest mainly to decide how many test runs of a certain sensor-method calculation are necessary to get a result that additional test runs are unlikely to change much. Therefore, the average dispersion over all test segments is used as stability measure. Unfortunately, to the best of the authors' knowledge, there is no common dispersion metric for numerical and ordinal scales. Thus, two different metrics had to be adopted, making results for ordinal and numerical methods incomparable. However, dispersion between different numerical or ordinal methods as well as between sensors combined with the same method are still possible.

For numerical assessment methods, the coefficient of variation CV is used as dispersion metric. As shown in Equation 7, it is calculated as the ratio of the standard deviation $δ$ to the mean $μ$ of the ratings per test segment. Also called the Normalized Root-Mean Square Deviation or relative standard deviation, it is a widely used standardized dispersion measure.

7

C V = \frac{δ}{μ}

For ordinal assessment methods, ordinal dispersion as defined by Blair and Lacy (2000) is used. Equation 7 shows the calculation of $l^{2}$ , a measure of concentration. For dispersion, the inverse $1 - l^{2}$ is used. In the formula, $F_{i}$ denotes the cumulative frequency, or sum of its own frequency and that of all lower classes, of the i-th class. From cumulative frequencies of all k classes but that of the highest class, 0.5 is subtracted, the result squared and these values summed. The highest class' cumulative frequency is dropped as it is always 1. Subtracting 0.5 yields a metric independent of the center of the distribution: if most samples are rated low, a cumulative frequency of 0.5 is reached fast, yielding increasing positive values for $F_{i} - \frac{1}{2}$ . If most samples are rated high, a cumulative frequency of 0.5 is reached slowly, yielding relatively high negative values for $F_{i} - \frac{1}{2}$ . Squared these become equal, yielding a method only dependent on the width, not the center of the distribution. $\frac{k - 1}{4}$ is used to get a normed metric. It is the highest possible value of the numerator for an ordinal metric with k possible classes. The highest possible concentration would mean all values in exactly one class. The numerator would then be a sum $k - 1$ -times either ${(0 - \frac{1}{2})}^{2}$ or ${(1 - \frac{1}{2})}^{2}$ , exactly the value of the denominator.

8

l^{2} = \frac{\sum_{i = 1}^{k - 1} {(F_{i} - \frac{1}{2})}^{2}}{\frac{(k - 1)}{4}}

Reliability calculation

The reliability of assessments made using a certain sensor-method combination is a metric whether applying this combination to a certain test route is likely to produce similar results as applying an ensemble of other combinations to the same test routes. This is of interest to decide whether one or the other method is more likely to produce a ‘realistic’ assessment of a given test route, assuming that an ensemble of established methods should produce a good assessment. As absolute values of different numerical and ordinal scales are hard to compare, relative assessments are compared instead. To this end, Spearman's rank correlation coefficient (Corder & Foreman, 2014) is calculated as follows:

First, for each predefined segment length, the assessments per sensor-method combinations are normalized.
Next, an average assessment of all sensor-method combinations is calculated for each segment.
Third, both the assessments per sensor-method combination as well as the average are ranked.
Last, Spearman's rank correlation is calculated between each sensor-method combination, all other combinations, and the average of all methods.

The resulting values represent the degree to which any given sensor-method combination will rank the test segments surface roughness in a similar order compared to the other methods and the ensembles average. The underlying assumption is that, while the absolute ratings of any method might depend on a multitude of factors, the ranking of segments should be comparable for any method considered to be able to produce a good assessment of surface roughness.

Results

The surface roughness assessments of different combinations of sensors, calculation methods, and segment lengths were compared using the methods described at the end of the previous section. The results are presented subsequently, starting with the stability of each method across the two sensors and four segment lengths. Next the reliability, defined as the agreement with the other methods and an averaged assessment of all methods, measured using Spearman's rank correlation coefficient, is discussed. Finally, some qualitative examples are presented, and the findings summarized and interpreted.

Stability

As pointed out in section 3 the stability of numerical and ordinal assessment methods are not directly comparable. As to the best of the authors knowledge, no dispersion metric applicable to both types of scales exists. However, to portray the effects of sensor and segment length, they are still displayed side by side in Figure 5. At the top of each of the four box plots, the method by Kranzinger and Leitinger (2021), denoted ‘Kranz.’, and the BEQI (Nuñez et al., 2020), the two ordinal methods, are shown. As described, the other three methods yield numerical assessments. As can be seen, the used method has the biggest impact on dispersion, consistent across sensor type and segment length.

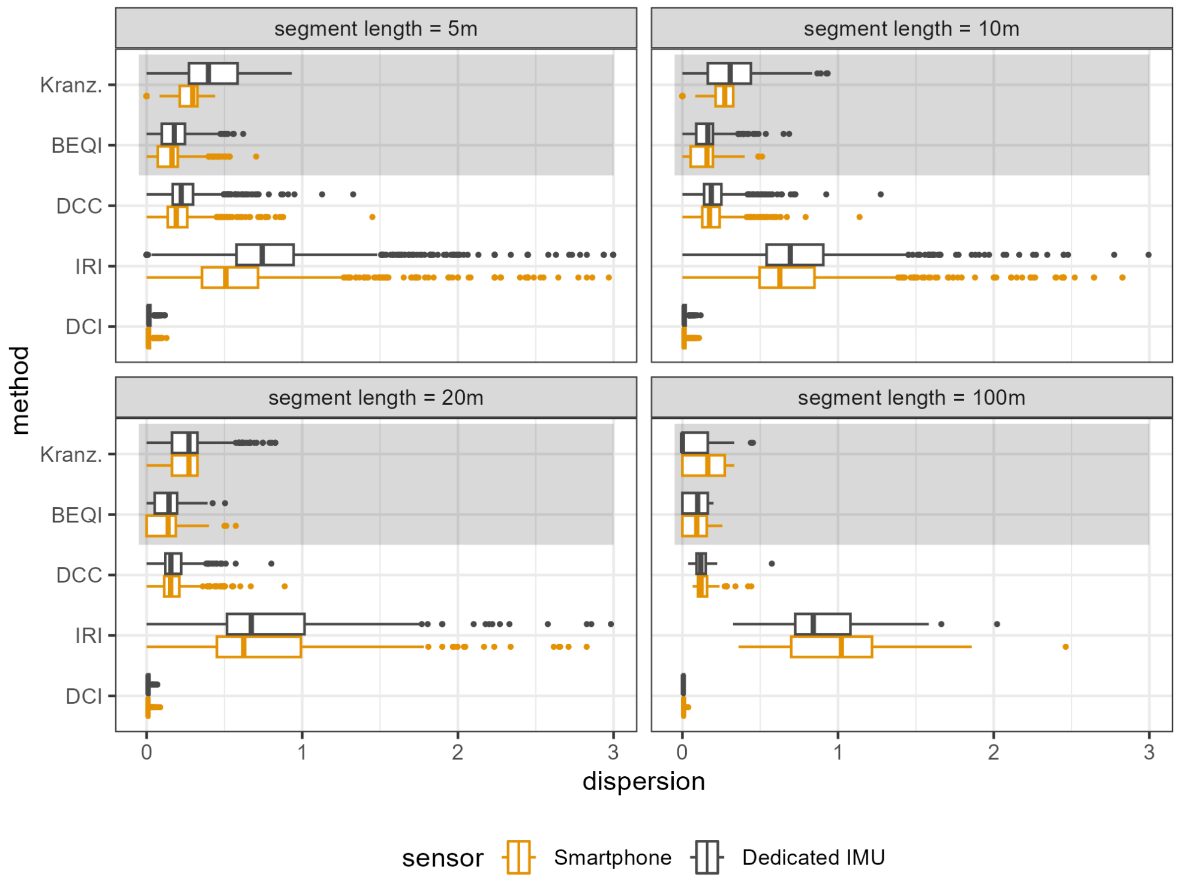
https://typeset-prod-media-server.s3.amazonaws.com/article_uploads/9098b204-d7db-48a4-98be-95290089f3fc/image/64b52bd0-d370-4f84-b9c7-b8f0eede1e4c-u5_beeking-without-yellow.png — **Figure 5: Distribution of the dispersion per segment with respect to sensor type, roughness calculation method combination and segment length (the grey highlighting marks the two ordinal methods)**

Of the ordinal methods, the BEQI is more stable and its dispersion is less impacted by sensor type than the assessment using the method by Kranzinger and Leitinger. Notably, the method by Kranzinger and Leitinger appears to be the least impacted by chosen segment length. Of the numerical methods, the DCI shows exceptionally stable results across both sensors and all segment lengths. The IRI, calculated as described by Zang et al. (2018) shows a very high dispersion, indicating highly unstable results across test runs. The DCC is somewhat in between, without particularly stable or unstable results. However, among the numerical methods it is least impacted by segment length.

Next, the segment length has a major influence on dispersion. Unsurprisingly, longer segments tend to yield more stable results, except for the IRI calculation as described by Zang et al. (2018). This was to be expected, as the longer the section is, the smaller is the impact of little differences in the actually driven path. For short segments, even single swerves hitting or avoiding any unevenness have a major impact. This is a disadvantage of any IMU-based method: only the surface directly beneath the tires can be assessed. Notably, as there are about 20 times less segments with a length of 100 m than with a length of 5 m, there are also a lot less outliers for longer segments.

For shorter segments, the assessments made using the XSens are in general less stable than the ones using a smartphone, with the exception of the combination with the DCI. This also indicates a bigger dispersion in the measured accelerations themselves. However, for longer segments, this effect disappears, likely due to the described ‘smoothing’ effect of adding more data points.

In conclusion, the most stable numerical assessments are achievable using the combination of dedicated industrial-grade IMU and the DCI method by Bíl et al. (2015). However, especially when using the DCI, the effect of the used sensor is neglectable. The least stable assessments are produced when calculating the IRI as described by Zang et al. (2018) based on measurements by the dedicated IMU. Of the ordinal methods, the BEQI is more stable, especially for shorter segments and when using the dedicated IMU for acceleration measurement.

Reliability

As described in section 3 the reliability of each method is defined as its agreement with the other methods, as well as an assessment averaged from all considered methods. Rank correlation is used to be able to properly compare numerical and ordinal assessment methods. All sensor-method combinations are correlated against each other as well as against the average assessment calculated as described in section 3. The correlations are depicted for the different segment lengths in Figure 6 to Figure 9. The resulting reliability metric ranges between 1 for total accordance, as seen in the correlation of each combination with itself; and -1 for exact opposite ranking of sections.

Notably, the DCI (Bíl et al., 2015), DCC (Gao et al., 2018), and BEQI (Nuñez et al., 2020) are all highly correlated. This is a result of them all being based on the root mean square of accelerations. The DCI only uses downward accelerations > 1 g, the DCC takes accelerations from all accelerometer axes and the BEQI projects the results onto an ordinal scale. But beyond that, they all use a root mean square of accelerations for vibration assessment as recommended by ISO 2631-1 (ISO, 1997).

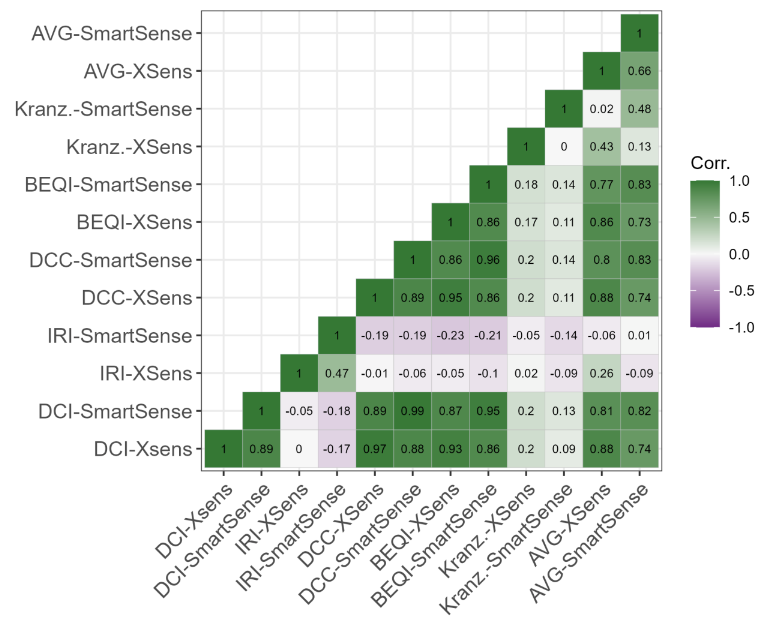
https://typeset-prod-media-server.s3.amazonaws.com/article_uploads/9098b204-d7db-48a4-98be-95290089f3fc/image/71f4b996-12c9-4bfe-90cc-6809911fa53c-ua_beeking.png — **Figure 6: Spearman's rank correlation coefficients matrix for a segment length of 5 m**

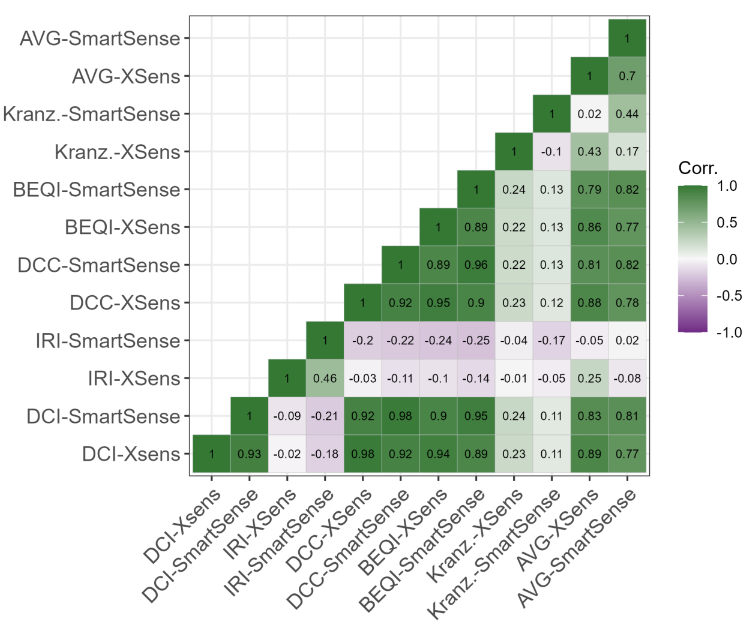
https://typeset-prod-media-server.s3.amazonaws.com/article_uploads/9098b204-d7db-48a4-98be-95290089f3fc/image/f594e8d0-0dd2-4ae9-9215-a3380748096d-ub_beeking.png — **Figure 7: Spearman's rank correlation coefficients matrix for a segment length of 10 m**

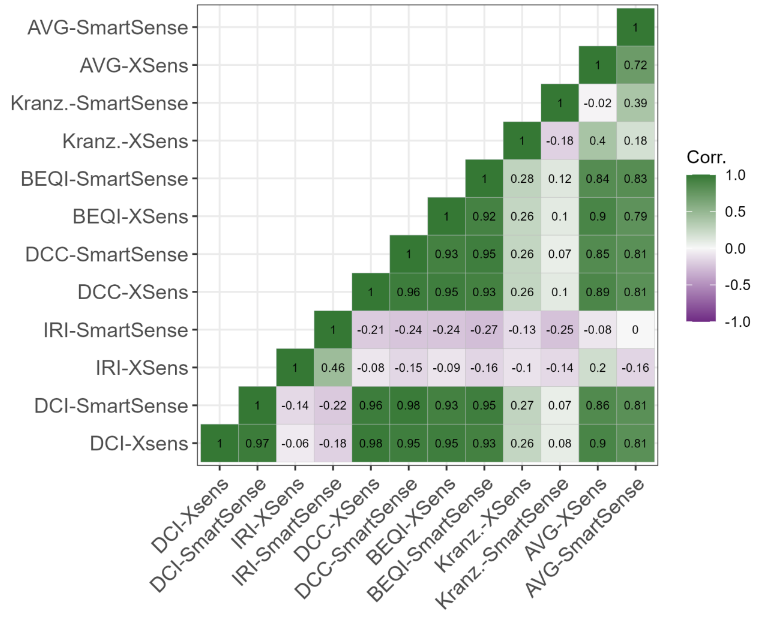
https://typeset-prod-media-server.s3.amazonaws.com/article_uploads/9098b204-d7db-48a4-98be-95290089f3fc/image/cba17bc8-adb3-4005-9f6c-8c43a6128d7f-uc_beeking.png — **Figure 8: Spearman's rank correlation coefficients matrix for a segment length of 20 m**

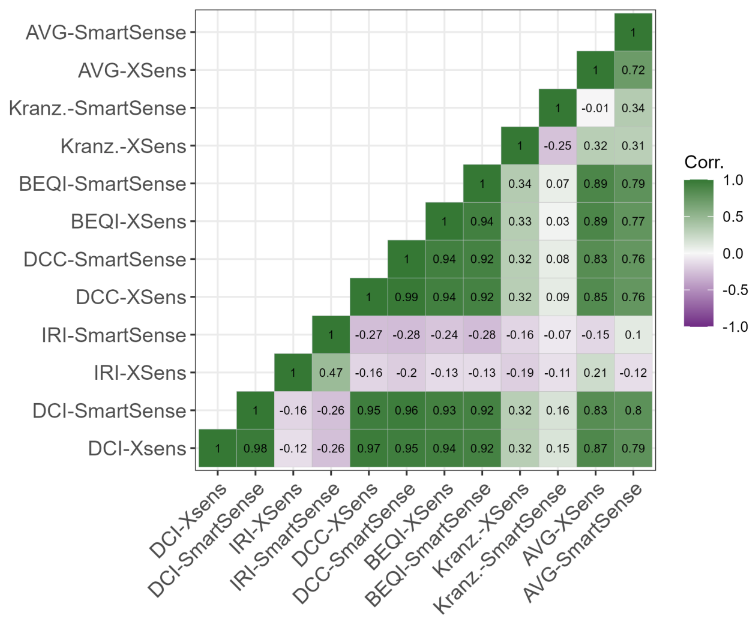
https://typeset-prod-media-server.s3.amazonaws.com/article_uploads/9098b204-d7db-48a4-98be-95290089f3fc/image/e112b0f1-2222-4274-8e98-72b8f7801005-ud_beeking.png — **Figure 9: Spearman's rank correlation coefficients matrix for a segment length of 100 m**

This yields a certain problem for taking the correlation with the averaged assessment as a reliability measure, as these three methods might appear disproportionately reliable. For future applications of this comparison approach, this might be alleviated by a more diverse selection of methods. For this work, the presented correlations need to be interpreted with due care.

Concerning the effect of segment length, longer segments yield a generally higher correlation of different methods. Especially between the 5 m segments and the 10 m segments, correlation improved for the majority of pairwise compared sensor-method combinations. Increasing the length further yielded small gains for 20 m segments, and somewhat inconclusive results for 100 m segments. Contrastingly, the correlation of the IRI, calculated as described by Zang et al. (2018), decreased with segment length. This indicates some kind of difficulty this method encounters with longer segments.

As with stability, the impact of the two different sensors decreases with segment length. Also, it is again highly dependent on the used roughness calculation method. The three aforementioned, root mean square based, methods show high correlations with themselves and towards each other for both sensors used. The IRI ranking is less correlated to the IRI ranking using the other sensor, however still more than to any other method. In general, the IRI is actually negatively correlated to all other methods, indicating some major problems of either the method or the used reimplementation.

The method by Kranzinger and Leitinger is most interestingly stronger correlated to other methods than to itself using another sensor, especially for longer segments. Its overall correlation to other methods is rather weak, although increasing with segment length. However, as mentioned three of the methods are based on the same fundamental concept of a root mean square of accelerations. The method by Kranzinger and Leitinger on the other hand is based on a clustering by mean jerks and share of heavy jerks. Jerks are defined as the derivative of the measured vertical acceleration. Presumably, this approaches' sensibility to few very high accelerations is different from the root mean square based approaches. Therefore, comparison to another method considered sound in itself would be required to achieve a trustworthy estimation of its actual reliability for surface roughness assessment. Interestingly, this method is hardly correlated to itself using a different sensor. Presumably, this is the result of the different heavy jerk thresholds and cluster centers calculated for the two sensors.

Qualitative example

As a minimal qualitative example of results, Table 2 lists the ranks of all methods for the on average best and worst assessed segments per segment length and used sensor. As can be seen, the agreement of methods for XSens measurements on these segments is generally high, especially for the good sections. Interestingly, the agreement decreases with segment length. As with stability and reliability, the IRI does not fare too well, again worse for longer segments. The ranks of the two ordinal methods in the last two columns are expected to be less clear, as for all segments in one class, an average rank is used. This also yields the 0.5 ranks.

Table 2: Ranks of the on average best and worst sections, calculated as described in 3.3.2, per segment length and sensor for all methods

Segment length	Sensor	Average rank	DCI rank (Bíl et al., 2015)	IRI rank (Zang et al., 2018)	DCC rank (Gao et al., 2018)	BEQI rank (Nuñez et al., 2020)	Kranz. rank (Kranzinger & Leitinger, 2021)
5	Smartphone	1.0 (Best)	328.0	37.0	158.0	200.0	137.0
		1 106.0 (Worst)	1 105.0	123.0	1 106.0	1 063.5	690.0
	XSens	1.0 (Best)	1.0	12.0	1.0	2.0	455.5
		1 080.0 (Worst)	1 071.0	791.0	1 072.0	1 041.0	1 073.0
10	Smartphone	1.0 (Best)	146.0	19.0	60.0	88.5	54.5
		559.0 (Worst)	558.0	318.0	557.0	536.5	334.0
	XSens	1.0 (Best)	1.0	6.0	1.0	1.0	244.5
		550.0 (Worst)	547.0	425.0	547.0	529.0	547.0
20	Smartphone	1.0 (Best)	42.0	124.0	49.0	40.5	21.0
		285.0 (Worst)	283.0	143.0	283.0	274.5	163.5
	XSens	1.0 (Best)	1.0	2.0	1.0	1.0	129.5
		280.0 (Worst)	265.0	50.0	263.0	270.0	279.5
100	Smartphone	1.0 (Best)	13.0	49.0	21.0	23.5	1.5
		57.0 (Worst)	56.0	23.0	56.0	56.0	30.0
	XSens	1.0 (Best)	5.0	9.0	4.0	7.0	28.0
		57.0 (Worst)	57.0	19.0	56.0	56.0	56.5

For accelerations measured using a smartphone, there is less of an agreement, especially for the good segments. Interestingly, for the good sections, the method by Kranzinger and Leitinger appears to yield better results, however this might also be a misinterpreted effect of the class distribution of the two ordinal methods. Furthermore, the best segments all feature asphalt in good condition, while the worst sections all feature rough cobblestone surfaces. This confirms the general assessments of the used methods. However, 16 out of about 4 000 segments can at best be used to get a general idea of the characteristics of each method. For proper analysis of the methods, quantitative approaches as described are required.

Discussion

The described reliability, stability, and exemplary qualitative results allow for some deductions. First and foremost, the selected method has the biggest impact on the resulting assessment, regarding both reliability and stability, well above the impacts of used sensor and segment length. This supports the ongoing research into better assessment algorithms. Furthermore, it sets the focus for any attempts at assessing infrastructure surface quality in a given area.

Second, segment length had a bigger impact on reliability than on stability. This indicates that using several measuring runs is a well suited approach to stabilize the outputs of the considered methods. As a side effect, the impact of the different sensors was less visible on reliability than on stability. However, it still mostly depended on the used method. Overall, except for the IRI, longer segments yield more similar assessments both per test run and also when comparing methods. On the other hand, they also decrease spatial resolution and might impede the detection of small problematic areas by a ‘smoothing’ effect.

Furthermore, the effect of different sensors, although dependent on segment length, can be considered to have a minor impact on the resulting assessment. Especially for the three root mean square based methods, results using either sensor were very comparable. For the IRI, the generally bad results are worse when based on smartphone measurements. Regarding the method by Kranzinger and Leitinger, it is interesting to note that there is little correlation when applying the method to the acceleration data collected using either sensor. However, as noted it is the only method with parameters tuned to each sensors measurements.

Last, the coherent results of both the stability and reliability measures indicate the chosen comparison methods to be well suited for the task at hand. This supports the assumptions leading to their selection and might be a useful finding for any future works aiming to compare their own, newly developed, methods to existing ones. As the described methods are mathematically well defined and straightforward to implement, little effort is needed to apply them in any such future works.

Conclusions

The aim of this work, as stated in the introduction, is to compare the assessments of the selected surface roughness calculation methods and sensors in order to provide recommendations for such assessments. To this end, acceleration measurements were conducted and the collected measurements assigned to different length segments. Based on these, roughness metrics were calculated using reimplementations of the selected metrics. These were then compared using specifically developed comparison methods. The results concerning stability, reliability, and results on selected segments were presented in the previous section. These yield the following recommendations for the usage of certain sensors and methods for surface roughness assessment.

First and foremost, the DCI developed by Bíl et al. (2015) yielded the most stable results across both sensors and all segment lengths, but especially for shorter segments. It was among the least affected by sensor selection and also among the highest correlated with all other methods. Furthermore, the method description in the original work is commendably concise and the used algorithm is straightforward and easy to implement. Therefore, the DCI emerges from this comparison as the recommended approach to assess surface roughness.

Next, the method to calculate the IRI as described by Zang et al. (2018) yielded very unstable results, which were also not correlated well with the other methods. Therefore, this method should not be used for roughness calculation unless two prerequisites are met: First, either through communication with the original authors or by extensive own exploration, a stable, reliable implementation of the method is found. To this end, the exact implementation of the double integration as well as possible filtering steps would need to be examined carefully. And second, high quality measuring equipment firmly attached to the bike yielding as little noise as possible needs to be used to alleviate the problem of high outlier sensibility. As these are two considerable obstacles, the method cannot be recommended despite its solid foundation in road maintenance and inherent elegance.

If an ordinal assessment is required, the BEQI (Nuñez et al., 2020) is both more stable and better correlated to the other methods than the method by Kranzinger and Leitinger (2021). However, as the BEQI only splits the root mean square of vertical accelerations at certain thresholds another viable option emerges: First, calculate the DCI as described by Bíl et al. (2015), then select fitting thresholds for an ordinal assessment based on the results.

The DCC as described by Gao et al. (2018) is neither particularly stable or unstable nor reliable or unreliable. It is therefore not recommended before or against, but considered a solid variant of ISO 2631-1 (ISO, 1997). This ISO standard however should at least be considered by any attempt at developing a surface roughness assessment method based on acceleration measurements.

Choosing the right segment length is another important consideration. As expected, the stability generally increased with longer segments. So did the correlation between methods, indicating a high reliability of assessments on longer segments. On the other hand, spatial resolution is lost and short problematic sections might be missed because of the ‘smoothing’ effect of longer segments. With the differences in correlation between the segment lengths in mind, 5 m and possibly shorter segments should only be chosen where absolutely required as they yield both unstable and somewhat unreliable results. Segments of 10 m to 20 m are both reasonable, so selection should be made based on the aforementioned criteria. Longer segments, especially 100 m and beyond yield limited gains in reliability and stability, and should only be used if the assessments need to be based on acceleration data of questionable reliability for some reason.

The impact of the different sensors on both stability and reliability is neglectable compared to both method and segment length. Therefore, a handlebar mounted smartphone can be concluded to be sufficient for bicycle infrastructure assessment. This furthermore confirms the applicability of smartphone-based crowd sourcing approaches for large scale infrastructure assessment.

Using acceleration measurements for roughness estimation is a well established and wide spread approach. Still, it is not without limitations that should be considered, especially when attempting large scale infrastructure assessment. These limitations, as described in detail in different sections throughout this document, are as follows: First and foremost, each test ride only captures the roughness directly beneath the tires. Therefore, any reliable assessment needs to be based on multiple rides on the same routes. Next, the measured accelerations are highly dependent on the type of bicycle used, the weight of the rider, the tire pressure, and the riding style, especially the speed. Thus, data from different sources is not directly comparable. This might be mitigated by sufficiently large numbers of measurements to work with averages instead of single test rides. Finally, using IMUs for roughness estimation does make distinguishing different reasons for roughness difficult. Cobblestone is barely different from unintentionally rough surfaces, manhole covers are hard to distinguish from potholes. If the reasons for roughness are to be considered, video based approaches should be considered.

The comparison approaches developed for this work proved usable and conclusive. One caveat is the effect of multiple similar methods in the comparison, increasing the apparent reliability of these works. However, this can be alleviated by careful selection of comparison methods. At the very least, a feasible way of comparing the reliability of ordinal and numerical assessment methods was presented. Unfortunately, the stability can only be compared among either ordinal or numerical assessments. Nonetheless, the presented approach constitutes a solid tool to select fitting segment lengths for surface roughness assessment methods.

Based on the presented research, several possible future research topics arise. The most obvious and easily achievable one would be to apply the comparison to additional methods from literature. However, the authors believe to have chosen reasonable representatives for the most common approaches, and therefore expect little additional value from doing so. More interestingly, based on the consideration that a handlebar-mounted smartphone is sufficient for surface roughness assessment, the effect of using different bikes could be properly quantified. Subsequently, suitable normalization methods could be developed to further advance crowd sourcing approaches. Lastly, the developed comparison methods could be used to develop yet more stable and reliable assessment approaches for high precision roughness mapping.

Funding

The research leading to these results has received funding from the Federal Ministry for Climate Action, Environment, Energy, Mobility, Innovation and Technology (BMK) under grant GZ 2021-0.641.557.

Declaration of competing interests

The authors declare no conflict of interests.

CRediT contribution statement

[1] Arthur, D., S. Vassilvitskii (2007), 'K-Means++ the Advantages of Careful Seeding', ACM-SIAM symposium on Discrete algorithms, New Orleans, LA, USA, 7–9 January 2007. https://doi.org/10.5555/1283383.1283494.

[2] Astarita, V., V. Rosolino, I. Teresa, G. Vincenzo, D. M. Francesco (2014), 'Automated Sensing System for Monitoring of Road Surface Quality by Mobile Devices', Procedia - Social and Behavioral Sciences, 111 https://doi.org/ 10.1016/j.sbspro.2014.01.057.

[3] Axhausen, W. K., R. L. Smith (1986), 'Bicyclist Link Evaluation: A Stated-Preference Approach', Transportation Research Record, 1085 http://onlinepubs.trb.org/Onlinepubs/trr/1986/1085/1085-002.pdf.

[4] Ayachi, F., J. Dorey, C. Guastavino (2014), 'Identifying Factors of Bicycle Comfort: An Online Survey with Enthusiast Cyclists', Applied Ergonomics, 46, 124, https://doi.org/10.1016/j.apergo.2014.07.010.

[5] Bíl, M., R. Andrášik, J. Kubeček (2015), 'How Comfortable Are Your Cycling Tracks? A New Method for Objective Bicycle Vibration Measurement', Transportation Research Part C: Emerging Technologies, 56 https://doi.org/10.1016/j.trc.2015.05.007.

[6] Blair, J., M. G. Lacy (2000), 'Statistics of Ordinal Variation', Sociological Methods & Research, 28(3) https://doi.org/10.1177/0049124100028003001.

[7] Calvey, J., J. P. Shackleton, M. D. Taylor, R. Llewellyn (2015), 'Engineering Condition Assessment of Cycling Infrastructure: Cyclists’ Perceptions of Satisfaction and Comfort', Transportation Research Part A: Policy and Practice, 78 https://doi.org/10.1016/j.tra.2015.04.031.

[8] Castañon, U. N., P. J. G. Ribeiro (2021), 'Bikeability and Emerging Phenomena in Cycling: Exploratory Analysis and Review', Sustainability, 13(4) https://doi.org/10.3390/su13042394.

[9] Corder, G. W., D. I. Foreman (2014), Nonparametric Statistics: A Step-by-Step Approach, (New Jersey, USA: John Wiley & Sons).

[10] CROW, (2016), 'Design Manual for Bicycle Traffic', (Rotterdam, the Netherlands: CROW-fietsberaad). Record 28,

[11] EC, (2023), 'Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions. Proposing a European Declaration on Cycling', Brussels, 4.10.2023 COM(2023) 566 final, https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:52023DC0566.

[12] Gadsby, A., J. Tsai, K. Watkins (2022), 'Understanding the Influence of Pavement Conditions on Cyclists’ Perception of Safety and Comfort Using Surveys and Eye Tracking', Transportation Research Record: Journal of the Transportation Research Board, 2676(12) https://doi.org/10.1177/03611981221090936.

[13] Gadsby, A., K. Watkins (2020), 'Instrumented Bikes and Their Use in Studies on Transportation Behaviour, Safety, and Maintenance', Transport Reviews, 40(6) https://doi.org/10.1080/01441647.2020.1769227.

[14] Gao, J., A. Sha, Y. Huang, H. Liqun, Z. Tong, W. Jiang (2018), 'Evaluating the Cycling Comfort on Urban Roads Based on Cyclists’ Perception of Vibration', Journal of Cleaner Production, 192 https://doi.org/10.1016/j.jclepro.2018.04.275.

[15] Harikrishnan, P. M., V. Gopi (2017), 'Vehicle Vibration Signal Processing for Road Surface Monitoring', IEEE Sensors Journal , 17(16) https://doi.org/10.1109/JSEN.2017.2719865.

[16] Hoelzel, C., F. Höchtl, V. Senner (2012), 'Cycling Comfort on Different Road Surfaces', Procedia Engineering, 34 https://doi.org/10.1016/j.proeng.2012.04.082.

[17] Holger, H., N. Ibesich, A. Kurzweil (2015), 'Cycling Master Plan 2015 - 2025', Federal Ministry of Agriculture, Forestry, Environment and Water Management, https://eionet.kormany.hu/download/7/a4/a1000/43_MP-Radfahren_englisch_web.pdf.

[18] ISO, (1997), 'Mechanical vibration and shock — Evaluation of human exposure to whole-body vibration', International Standards Organisation, ISO 2631-1:1997, https://www.iso.org/standard/7612.html.

[19] Kranzinger, S., S. Leitinger (2021), 'Eine Bestimmung der Oberflächenqualität von Fahrradinfrastruktur durch Smartphone-Beschleunigungsdaten mithilfe des k-means++-Algorithmus [A Determination of the Surface Quality of Bicycle Infrastructure from Smartphone Acceleration Data Using the k-means]', Journal für Angewandte Geoinformatik, 7 https://doi.org/10.14627/537707013.

[20] Landis, B. W., V. R. Vattikuti, M. T. Brannick (1997), 'Real-Time Human Perceptions: Toward a Bicycle Level of Service', Transportation Research Record, 1578(1), 119–126, https://doi.org/10.3141/1578-15.

[21] Litzenberger, S., T. Christensen, O. Hofstätter, A. Sabo (2018), 'Prediction of Road Surface Quality during Cycling Using Smartphone Accelerometer Data', Proceedings, 2(6), 217, https://doi.org/10.3390/proceedings2060217.

[22] Neto, V. A. G., J. D. F. Viana, R. B. Braga, C. T. Oliveira (2018), 'Surfaces Categorization Based on Data Collected by Bike Sensors', Euro American Conference on Telematics and Information Systems, Fortaleza, Brazil, 12–15 November 2018. https://doi.org/10.1145/3293614.3293625.

[23] Nuñez, J. Y. M., D. R. Bisconsini, A. N. R. da Silva (2020), 'Combining environmental quality assessment of bicycle infrastructures with vertical acceleration measurements', Transportation Research Part A: Policy and Practice, 137, 447–458, https://doi.org/10.1016/j.tra.2018.10.032.

[24] Olieman, M., R. Marin-Perianu, M. Marin-Perianu (2012), 'Measurement of Dynamic Comfort in Cycling Using Wireless Acceleration Sensors', Procedia Engineering, 34 https://doi.org/10.1016/j.proeng.2012.04.097.

[25] ÖVDAT, (2022), 'Die Graphenintegrations Plattform GIP. Das Referenzsystem der öffentlichen Hand für Verkehrsinfrastrukturdaten [The graph integration platform GIP. The public sector reference system for transport infrastructure data]', Österreichisches Institut für Verkehrsdateninfrastruktur, https://www.gip.gv.at/, accessed 2024-11-09.

[26] Rehrl, K., S. Gröchenig, M. Wimmer (2018), 'Optimization and Evaluation of a High-Performance Open-Source Map-Matching Implementation', in Mansourian, A., P. Pilesjö, L. Harrie, R. van Lammeren (eds.), Geospatial Technologies for All, (Cham, Switzerland: Springer) https://doi.org/10.1007/978-3-319-78208-9_13.

[27] Sayers, M. W., M. S. Karamihas (1998), The Little Book of Profiling, (USA: University of Michigan) https://hdl.handle.net/2027.42/21605.

[28] Taylor, M., C. A. Fairfield (2010), 'Intelli-Bike: A Cycling Infrastructure Asset Management System', Proceedings of the Bicycle and Motorcycle Dynamics 2010. Symposium on Dynamics and Control of Single Track Vehicles, Delft, The Netherlands, 20–22 October 2010, http://bicycle.tudelft.nl/bmd2010/.

[29] UN, (2024), 'Cycling and Sustainable Development Goals', United Nations Regional Information Centre for Western Europe, https://unric.org/en/sustainable-development-goals-cycling/, accessed 2024-11-20.

[30] Wijerathne, N., S. K. Viswanath, M. S. Hasala, V. Beltran, C. Yuen, H. B. Lim (2018), 'Towards Comfortable Cycling: A Practical Approach to Monitor the Conditions in Cycling Paths', IEEE World Forum on Internet of Things, Singapore, 5–8 February 2018. https://doi.org/10.1109/WF-IoT.2018.8355173.

[31] Yamanaka, H., S. Namerikawa (2007), 'Measuring Level-of-Service for Cycling of Urban Streets Using ‘Probe Bicycle System’', Journal of the Eastern Asia Society for Transportation Studies, 7 https://doi.org/10.11175/EASTS.7.1614.

[32] Yamanaka, H., P. Xiaodong, J. Sanada (2013), 'Evaluation Models for Cyclists’ Perception Using Probe Bicycle System', Journal of the Eastern Asia Society for Transportation Studies, 10 https://doi.org/10.11175/EASTS.10.1413.

[33] Zang, K., J. Shen, H. Huang, M. Wan, J. Shi (2018), 'Assessing and Mapping of Road Surface Roughness Based on GPS and Accelerometer Sensors on Bicycle-Mounted Smartphones', Sensors, 18(3) https://doi.org/10.3390/s18030914.