Reliability of C-ADAS and the importance of the acceleration function for cycling safety
Guest editor: Arend Schwab, Delft University of Technology, the Netherlands
Reviewers: Katja Kircher, Swedish National Road and Transport Research Institute, Sweden
Anonymous Reviewer, not disclosed due to disagreement with the editor's decision
Received: 23 January 2024; Accepted: 13 November 2024; Published: 3 December 2024; Updated: 4 December 2024 (formatting issues)
Abstract
Driving characteristics of bicyclists and motorists differ significantly in critical, uncritical and unaffected situations in road traffic. When bicyclists cross the path of right-turning motorists, bicyclists seem to mitigate conflicts that can develop into crashes, while motorists seem to avoid non-critical but close interactions that can develop into conflicts. This is one of the key findings of the evaluation of a recently developed and successfully tested cooperative driver assistance system (C-ADAS) that warns right-turning motorists of potential collisions. The warning is given by a special traffic light, which we called ‘amber light’, lighting up only in dangerous situations. Whether a situation becomes dangerous or not is determined by a decision tree, fed by the measured kinematics and specific surrogate measures of safety of the interacting road users. Most notably, the results demonstrate that criticality can be rated by measuring anticipation (or surprise) by computing the cross-power spectrum and applying entropy metric on the acceleration functions of the road users. However, one of the outcomes is that the time for the road users to perceive the amber light state might be too low to react properly. These findings can be used to improve the performance of such a C-ADAS.
Keywords
cooperative ADAS (C-ADAS), crash prevention, cross-power spectrum, cycling safety, entropy, traffic conflict analysis
Introduction
Cycling has become increasingly important in the decarbonisation of transport. However, the number of crashes involving bicyclists, which may go along with severe injuries or fatalities, is increasing. In Germany, the number of killed bicyclists increased from 381 to 474 (+24.4%) during 2010 to 2022 (Destatis, 2022), as in other parts of the world. In case of road user crashes with personal injury involving bicyclists in 2020, motorists most often make mistakes when turning (15.4%), give way (13.4%) and keep distance (12.6%) (Destatis, 2022), while bicyclists often use the wrong roadside (16.7%), make mistakes turning (8.1%) or give way (7.4%) (eBikeers, 2020). The interaction of right-turning motorists with crossing bicyclists is one of the most critical ones, particularly if the bicyclist is relatively behind the motorist (i.e. in its blind spot) (Kircher & Ahlström, 2020). In Kolrep-Rometsch et al. (2013), 66% of bicycle-vehicle crashes with personal injury were situations between right-turning motorists and crossing bicyclists. Obviously, there is an urgent need to completely avoid or at least mitigate such dangerous interaction situations between bicyclists and motorists by increasing situation awareness of the interacting road users. Consequently, at least the heavier road user (e.g. lorry) has to be aware of the situation in order to reduce speed to reduce kinetic collision energy in time and thus, accident severity of the bicyclist and to increase the remaining time for the bicyclist to conduct a potentially necessary evasive action.
Many efforts have been made to make cycling safer, some of them will be briefly described in section 2. One solution was recently presented by Saul et al. (2021), which will be the basis for this article. Saul et al. (2021) developed and Manz et al. (2020) successfully tested an algorithm for C-ADAS, which could predict potential crashes between right-turning motorists and crossing bicyclists and send out warnings to them. For this purpose, an infrastructure-based traffic light, called ‘amber light’, was used (Figure 1, right). If a potentially critical situation was predicted, the amber light lit up to warn the motorists before turning right, and it remained off for uncritical situations. Sending out warning messages was triggered by a decision tree (Figure 1, left) trained with the relevant variables describing such interaction situations: the distances of the bicyclists and motorists (dCP ) to their collision/conflict point (CP), their speeds (v) and predicted post-encroachment time (pPET) (remark: pPET continuously quantifies how narrowly motorists and bicyclists will have missed each other). This rule-based approach warned the interacting road users if certain conditions were exceeded. For instance, if dCP of the road users were below 17 m and pPET below 2 s and the speeds were larger than 1 m/s, a warning message was sent and the amber light lit up. A hysteresis prevented the amber light from changing states and thus, avoid switching on and off too often.
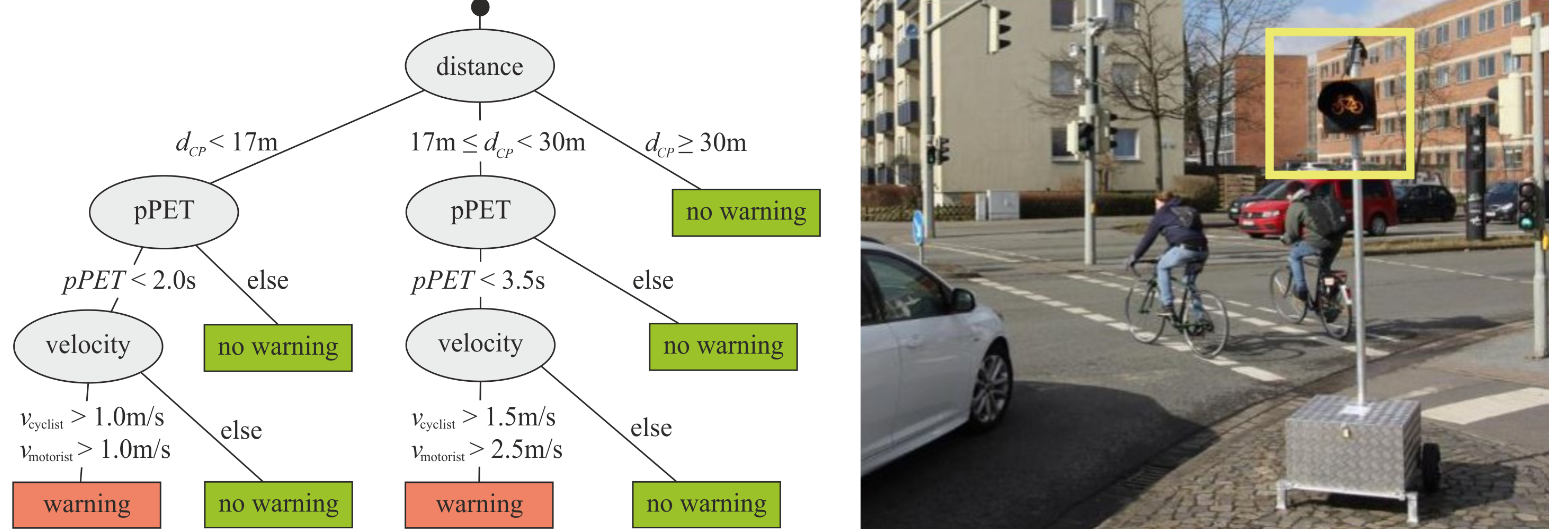
Although some behavioural patterns and positive effects of this C-ADAS were already presented in Dotzauer et al. (2018)—for instance, it could be shown that this implementation made this type of interaction between bicyclists and right-turning motorists approximately 11% safer—some unanswered problems remained. For instance, it seemed that road users' accelerations did not play a role for training the decision tree, although they are the only control parameters—apart from the change of direction—to perform evasive manoeuvres. In this respect, we will (i) show the largely differing kinematic characteristics between right-turning motorists and crossing bicyclists in critical and uncritical encounter situations and make use of them to measure anticipation (or ‘surprise’) in such encounter situations. Further, despite its above-mentioned positive effect on safety, this C-ADAS' reliability is almost completely unknown, particularly when dCP is considered. Therefore, we will evaluate it with regard to (ii) the reliability of just-in-time warnings before a potential collision between right-turning motorists and crossing bicyclists and (iii) the distance to CP such an amber light ought to be installed. These are examples of essentially important aspects to establish well-accepted C-ADAS in the future.
The article is organised as follows: A literature review about increasing situation awareness, relevant approaches to measure, predict and increase traffic safety as well as currently available ADAS is given in section 2. Then, in section 3, the methodical approach is presented that includes data collection at an urban intersection and required methods and metrics to conduct this study. Dedicated results are presented in section 4, which are discussed in section 5. In section 6, the article is concluded and aspects of our future work are presented.
Related work
Increase situation awareness
Road traffic regulations must be obeyed by all road users in order to ensure safe and efficient transport of people and goods. Participating in traffic requires a high level of vigilance. While ensuring situation awareness in traffic is the purpose of road traffic regulations and educating all road users of any age and type, it is quite a challenging task when it comes to technically increase situation awareness before upcoming collisions. Due to the spatio-temporal dynamics of traffic and its participants, critical situations and collisions are often the result of the wrong or inappropriate behaviour of road users interacting with other road users (Knake-Langhorst et al., 2024), if ‘something goes wrong’. As we know by the numbers of road user crashes, educating people and road traffic regulations are not sufficient to reduce road violence and road users being killed or seriously injured.
To increase road users' situation awareness technically, several ways of how to support road users in terms of the different levels of criticality of upcoming collisions have been discussed (5GAA, 2024; ETSI, 2013; Ihlström et al., 2019): The first level is informing the (potentially) interacting road users, without being on a collision course, about their presence. The second level is characterised by increasing situation awareness of road users on a collision course in case of a further escalation, but with time enough to avoid a collision. The third level is warning the road users, of which at least one of the road users has to adapt to the situation and conduct an evasive action to avoid a collision. The fourth and fifth levels can be described as technically assistance or intervention to avoid or minimise the consequences of a collision. Clearly, levels one, two and three can be handled by the road users without technical support, as they are not time critical. For instance, von Sawitzky et al. (2022) found that 6 to 9 s before a critical situation are reasonable to inform (level one) the driver in case of a dooring situation. Prohn and Herbig (2023) identified 2 s and McGehee and Carsten (2010) 1.8 s time for the levels two and three. In case of levels four or five, advanced driver assistance systems (ADAS) are necessary, because of their time criticality, which is very often less than 1 s.
ADAS and C-ADAS
Advanced driver assistance systems (ADAS) have been developed to assist drivers—mostly motorists—in several different traffic situations such as parking, lane-keeping, car-following, overtaking, and controlling energy consumption, etc. but particularly they should support drivers in critical situations before they develop into crashes. Collision warning systems for trucks is one example (Ulrich et al., 2020) of many other solutions and products. The European Parliament recently set implementation dates of vehicle-based collision avoidance systems for newly registered trucks and buses to July 2022 and for all new cars to July 2024 (EU, 2019). Solutions to support motorcyclists (Huang et al., 2022) and specifically bicyclists to avoid crashes become more and more popular, such as the BlincBike system (Christian, 2021) or Garmin's distance radar (Garmin, 2023), which can support the bicyclist to increase situation awareness and thus, reduce reaction time. The start-up company Borèal Bikes provides HolosceneX, a sensed (front/heck lidar and camera, heck radar) and V2X-equipped e-bike (Borèal Bikes, 2017) that uses smart grips with a Bluetooth based handlebar plugin for haptic feedback, bike tracking, hands free navigation, separation alerts, etc. (SmrtGRiPS, 2023). The bicycle manufacturer Canyon recently announced volume production of V2X technology in premium e-bikes (Gerteis, 2023). In Reallabor Hamburg (2022) a vehicle-to-anything-communication (V2X) based collision warning system was developed to warn the interacting road users before potential collisions. Lefèvre et al. (2012) validated a Bayesian approach to risk assessment among interacting motorists at intersections considering drivers' expectations in accordance with traffic regulations and their intentions. Estimated risks were sent to the road users by vehicle-to-vehicle communication (V2V).
Infrastructure-based solutions (i.e. cooperative ADAS or C-ADAS) that estimate an upcoming collision by a roadside unit send out warnings to the interacting road users or to a dedicated traffic light via infrastructure-to-vehicle-communication (I2V), can rarely be found on the market. The Bike Flash is an example of such a solution (Bike-flash, 2016), although it does not take advantage of I2V. Another C-ADAS solution was put into operation in Hamburg, Germany, recently (PrioBike-HH, 2024). Nine ground lights indicate to right-turning motorists that bicyclists are crossing. Although such systems should support right-turning motorists not to collide with bicyclists, they can lead to acceptance problems and negative consequences, if possible dangerous or safe outcomes of the situations are not considered. A drawback is that motorists might get warned although they already took notice of the bicyclists and thus get annoyed of superfluous information. As a consequence, motorists may learn to rely solely on the warnings instead of being alerted in such situations, what can even lead to larger negative consequences. In order to prevent motorists from learning to solely rely on warnings (if they have already taken notice of the bicyclists) and to warn only in the event of real danger, Saul et al. (2021) developed and Manz et al. (2020) successfully tested a C-ADAS that predicted potential collisions between right-turning motorists and crossing bicyclists. This system warned the interacting motorists only in the case of potentially critical situations. They used road user kinematics and the pPET as essential metrics to predict dangerous situations.
Estimation and prediction of conflicts and crashes
Typically, road safety is determined on the basis of crash data by considering the number and severity of crashes. But this method is disadvantageous due to the rareness and to some extent also randomness of crashes at certain locations. One more issue with using crashes or related indicators as a measure for road safety, especially in relation to active road users, is that certain road types are avoided by active road users. So, the absence of conflicts or crashes does not mean that such places are safe. Furthermore, the cause-effect-relationship cannot always be determined due to missing statistical significance making it a challenge to develop models explaining, predicting and preventing crashes in the future. For instance, crash prediction models (CPM) are used to model and estimate the number of crashes at a certain location considering traffic parameters (e.g. annual average daily traffic), infrastructural and other relevant parameters (e.g. number and width of lanes, available traffic control, etc.— Hossain et al. (2019)). Obasi and Benson (2023) evaluated the effectiveness of several machine learning techniques for crash severity prediction on the basis of several years of crash data. They found that random forest-based methods outperformed many other tested models by a prediction accuracy of 87% and additionally, across several injury severity classes. Based on observations, Tarko (2019) bridged the gap between crashes and conflicts by estimating the number of crashes given a certain number of conflicts within a time margin using the Lomax distribution.
The Swedish traffic conflict technique is an established method (Hydén, 1987; Laureshyn & Várhelyi, 2018). It allows understanding near-crashes, critical and non-critical encounters instead of only trying to analyse crashes. The drawbacks of the original traffic conflict technique are subjectivity and the missing valid quantification of the correlation between crashes and critical encounters, which have been overcome since technological advances in video-based systems and AI-based methods lead to better tracking and discrimination of traffic objects. Automated video-based detection and semi-automatic assessment of traffic situations allow for identifying critical traffic situations before they develop into crashes. The determination and application of so-called surrogate measures of safety (SMoS) by video-based traffic analysis (Ismail et al., 2010) is an opportunity to identify, analyse and understand safety-critical encounters or even crashes. Some SMoS can be used to evaluate traffic situations offline in post hoc analyses, while others are to suitable for online processing or even prediction tasks. For instance, TTC (time to collision), pPET (predicted post-encroachment time), T2 (measure that combines pPET and TTC) and extended Delta-V are examples that allow to determine and even forecast traffic situations and their possible outcomes in terms of severity. An example of the use of SMoS is the research presented in Saul et al. (2021) that developed an algorithm capable of discriminating between critical and non-critical encounters of right-turning motorists and crossing bicyclists using pPET, their distances to CP and their speeds.
Kluger et al. (2016) used trajectories of single vehicles of interacting road users of the SHRP2 Naturalistic Driving Study data set (SHRP2, 2013) to detect safety-critical events (i.e. crashes, near-crashes and other unsafe driving behaviours). They successfully identified 78% of the safety-critical events by analysing frequency time series of road user trajectories. Specifically, they transformed longitudinal acceleration data of the road users into Fourier space, computed the area under amplitude and performed and evaluated a k-means cluster analysis.
Conclusion
So far identified, C-ADAS for right-turning motorists and crossing bicyclists are rare and some of them lack adaptiveness. The recently developed C-ADAS (Saul et al., 2021) appeared to be the only one trying to warn the right-turning motorists by sending out warnings to them if potentially dangerous situations were predicted. However, its reliability is almost completely unknown and deserves more attention. This specific C-ADAS will be the basis for the research presented throughout this article. Besides consideration of road users’ kinematics and criticality metric pPET, we additionally will build upon the work of Kluger et al. (2016) (last part of section 2.3) and analyse the longitudinal acceleration functions of right-turning motorists and crossing bicyclists in unaffected, uncritical and critical encounter situations.
Methodological approach
This research makes use of recorded trajectories of right-turning motorists interacting with crossing bicyclists at an urban intersection. Apparatus and final data set are introduced in section 3.1. In section 3.2 we introduce the relevant methods and metrics to obtain answers concerning the role of the road users' acceleration functions with regard to cycling safety and the reliability of C-ADAS in question. This includes the computation of confusion rates over distance to CP, the pPET-function, while considering kinematic patterns of the road users as well as the application of specific signal processing methods, such as cross-correlation and Fourier transform. It appeared that the maxima of the cross-power spectra were suitable markers to significantly distinguish between critical, uncritical and unaffected situations. Since critical situations may occur as a surprise—because the involved road users do not expect them to happen and thus, react by evasive actions, such as braking or dodging, we expect acceleration functions of critical situations to differ characteristically from acceleration profiles of uncritical situations. Therefore, we will try to measure ‘surprise’ by applying the entropy metric on the acceleration functions. Finally, we will conduct inferential statistical tests on the relevant data.
Apparatus and final data set
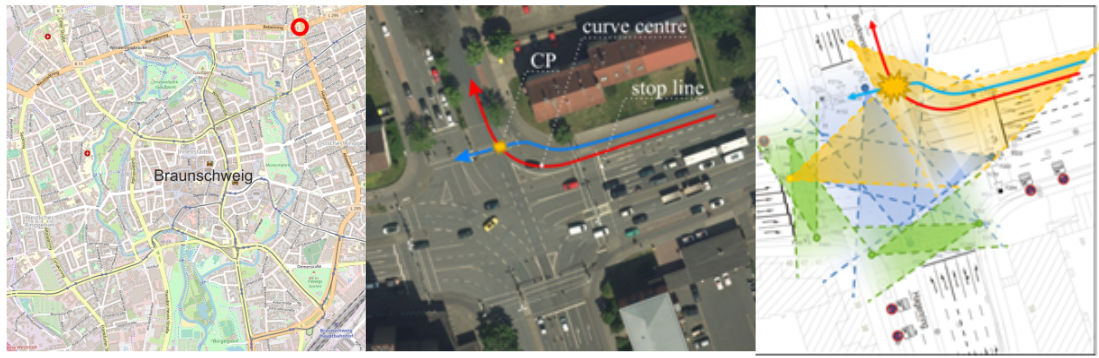
Trajectory and video data of bicyclists and motorists were recorded at AIM research intersection (Figure 2). This is a four-legged signalised urban crossing located at the north-eastern arm of the ring road in Braunschweig, Germany, equipped with stereo-cameras (Knake-Langhorst & Gimm, 2016). Approximately 20 000 road users pass this intersection every day (Saul et al., 2021).
Right-turning motorists and crossing bicyclists were recorded with 25 fps between 22 August and 18 September 2016 (four weeks) and between 28 May and 3 June 2018 (one week). The 2016 data set was used to train the decision tree (Saul et al., 2021), while this one week of the 2018 data was part of a five-week operation of the C-ADAS to increase the number of unaffected situations for the comparison (see below). Trajectory data consisted of GNSS-based time stamps, UTM positions, velocities, accelerations, headings (derived by adequate motion models and Kalman filtering), modes of transportation (e.g. car, truck, bicycle) and their sizes. Video data was anonymised in real-time to very low-resolution images to fulfil the European General Data Protection Regulation (GDPR, 2016) restrictions.
Altogether, trajectories of 1 169 crossing bicyclists and 12 305 right-turning motorists were recorded. The decision whether two road users interact with each other was made by filtering the trajectories with PET < 2.5 s. 49 conflict and 273 uncritical encounter pairs remained for further analysis after expert annotation (critical vs uncritical encounters), eventually. The conflict area was crossed by the motorist before the bicyclist in 85% of the critical encounters. The relation in case of uncritical encounters was the opposite, which means, in 89% of the cases the bicyclist crossed before the motorist. Additionally, 96 unaffected bicyclist and 836 unaffected motorist trajectories were recorded. Unaffected road users were the ones that were solely present on the crossing and thus, being completely undisturbed. Due to corrupted data (e.g. broken trajectories, missing time stamps, false detections such as bicyclists riding too close to each other) some trajectories were dismissed from the analysis. Sometimes trajectory data close to the collision point was missing. To calculate pPET, we extended those trajectories by 10 data points (i.e. 0.4 s) assuming that those road users went on at the same speeds as before. This also includes a compromise between preferably completed data and timely trajectories reflecting the road users' actual interaction behaviour. Finally, 40 critical, 237 uncritical and 96 unaffected pairs remained in the final data set (those 96 of 836 unaffected motorist trajectories were chosen at random).
Explorative observation
Situations with right-turning motorists from East to North interacting with crossing bicyclists from East to West were of specific interest. Both road user types shared the same traffic light phase and intersected the bicycle and pedestrian crossing. Critical encounter situations could appear when the interaction partners passed through the joint conflict area at the same time. To get an impression of the situations analysed, in Figure 3, three frames of a critical encounter situation are shown. Motorist C0 yielded bicyclist B31, but did not yield the approaching bicyclist B49 and started to accelerate. B49 had to resolve the conflict by braking and letting C0 pass with PET = 1.21 s (see explanation of PET in section 3.2.1 and Figure 4).

Kinematic patterns and predicted post-encroachment time
We computed kinematic patterns (i.e. speed and acceleration) of motorists and bicyclists and the pPET (known as Tadv in Hansson (1975)), which quantifies how close two interacting road users will have missed each other that shared the same conflict area. The pPET is also used to describe the implicit negotiation between bicyclists and motorists before passing through the shared area (Zhang et al., 2022). It is a suitable metric to estimate potentially dangerous situations of road user interactions and thus, predict critical situations or crashes. It can be computed during the whole interaction process by Equation 1 with expected travel time Ti , distance to CP di ,CP , speed vi of road user i = {1;2} and time t:
The pPET is different from post-encroachment time (PET). PET quantifies how close two interacting road users that shared the same conflict area have missed each other (Allen et al., 1978) (Figure 4). PET cannot be determined before, but always after a conflict or collision. However, pPET and PET are equivalent, if road users' paths to CP, their object sizes are known and their expected travel times Ti are continuously computed as shown in Equation 1.

Decision tree and confusion rates
The decision tree proposed in Saul et al. (2021) (Figure 1, left) was evaluated by determining the confusion rates along dCP . Sensitivity (true positive rate, TPR) and specificity (true negative rate, TNR) provided the percentage of the situations in which the C-ADAS in question correctly estimated conflicts and non-conflicts, respectively. Further quantities for the evaluation were overestimation and underestimation of conflicts. Overestimation is the percentage of predicted conflicts that were no conflicts (false-positive rate, FPR). Underestimation is the percentage of predicted non-conflicts that actually were conflicts (false-negative rate, FPN).
Correlation function and power density spectrum
The acceleration functions of unaffected, uncritical and critical situations were considered as stochastic signals with x(n) as bicyclist's and y(n) motorist's discrete acceleration functions, as time shift, as angular frequency, as imaginary unit and E as expectation value operator. Auto-correlation functions (ACF) and were computed, which reflect the magnitude of self-correlation and situation-specific mean signal energies at their maxima and (Unbehauen, 2002):
The cross-correlation function (CCF) was computed to identify the similarity of the acceleration functions between bicyclists and motorists:
In analogy to the ACFs in Equation 2 , the positions of their cross-correlation maxima and the situation-specific ‘cross-signal energy’ at were determined. Finally, was transformed into Fourier space using Discrete Fourier Transform to obtain the cross-power density spectrum RXY with as time shift, j as imaginary unit and as angular frequency):
Since the height of the maximum of ACF reflects the signal energy we applied this idea on CCF too to obtain RXY, max .
Entropy
In information theory, entropy H(a) is a measure of uncertainty, surprise or information of a stochastic variable a (here: acceleration) inherent to the variable's possible outcomes (Shannon, 1948). Due to the fact that accidents, critical (or atypical) situations in road traffic are rare events, the involved road users may be surprised by the situation and react by evasive actions, such as immediate braking or dodging. For this reason, we aim to measure anticipation (or ‘surprise’) by determining and comparing entropy of the acceleration functions for unaffected, uncritical and critical encounter situations. In our case, entropy H(a) will be computed with the symbols ai of the ‘acceleration alphabet’ (i.e. ), their probabilities pi = pi(ai) for each symbol and the dual logarithm ‘log2’ as:
Note that the maximum entropy and the probabilities pi change in dependence on the binnings of the alphabet. Therefore, entropy has to be robust against different alphabet binnings.
Inferential statistical tests
Methods of descriptive and inferential statistics with a level of significance of = 0.05 were applied to the obtained results. All relevant variables were tested for normality of the residuals by applying Shapiro-Wilk test. Some of the data samples were significant to reject the normality assumption. Data of speed, acceleration, pPET, entropy and the maxima of the cross-power density spectra were tested for homoscedasticity. Due to the different sample sizes, dependency on dCP and the violation of the homoscedasticity condition, non-parametric Mann-Whitney-U and Kruskal-Wallis-H tests were used for single and group comparisons, respectively. In case of post hoc tests, Bonferroni correction was applied.
Results
Preparation of final data set for analyses
The final data set (section 3.1) of unaffected, uncritical and critical situations had to be pre-processed for different purposes in different ways. In case of computing the ACFs , and CCF as well as the cross-power density spectrum RXY , the acceleration functions of bicyclists and motorists appeared to be characteristically different only at the last meters before CP. Consequently, all trajectories were cut at some distance before their CP and the parts from the cut to the CP remained. However, at what distance before CP those trajectories had to be cut, was part of this research. Actually, these limiting values were the result of the potential collision predictability in accordance with the outcomes of the interaction behaviour predicted post-encroachment time pPET, entropy H and cross-power density spectrum RXY (sections 4.3, 4.4 and 4.5). For this reason, 40 critical, 237 uncritical and 96 unaffected trajectory pairs remained. For statistical evaluation we balanced (Bortz & Schuster, 2010) the remaining data sets yielding a 1:2 fraction of 40 critical, 80 uncritical and 80 unaffected pairs, which were chosen randomly from the existing data pairs.
Confusion rates
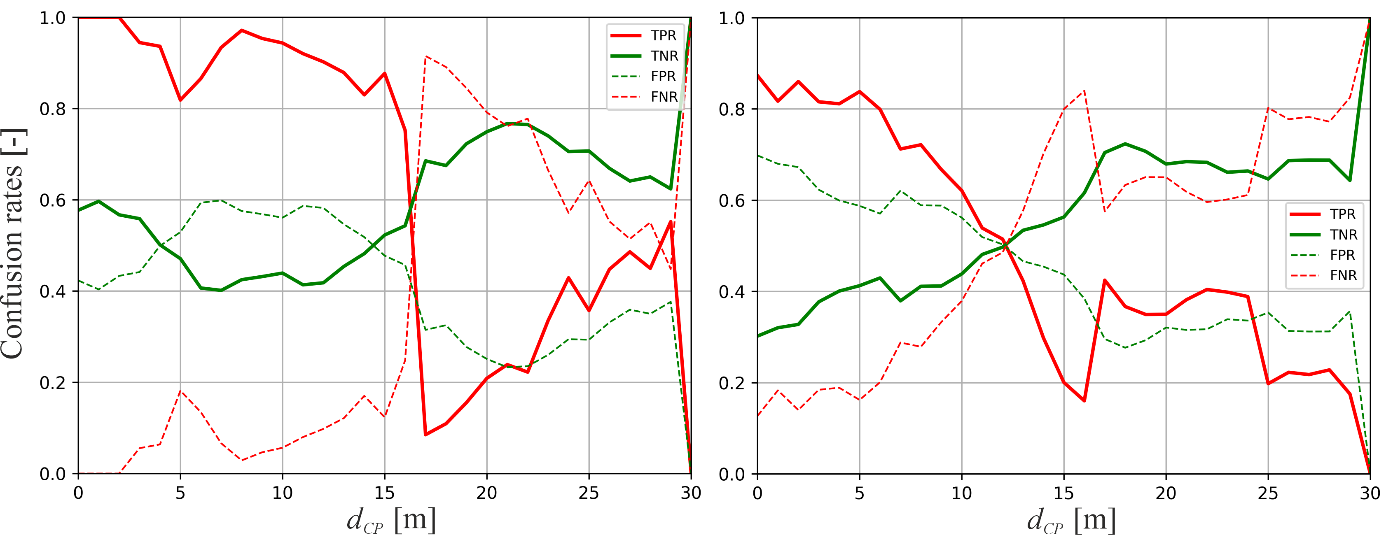
To evaluate reliability of C-ADAS in question (Figure 1, left), we computed the confusion rates for bicyclists and motorists along dCP (Figure 5):
-
Sensitivity (TPR)—a correct prediction of conflicts—shown as red solid line, appeared to exceed 50% after 16 m (bicyclists) and 12 m (motorists) before CP.
-
Specificity (TNR)—a correct prediction of non-conflicts—shown as green solid line, appeared to be approximately 40 to 60% in close range to CP and 70 to 80% at larger distances to CP.
-
Overestimation (FPR)—non-conflicts predicted as conflicts—shown as green dashed line, appeared to be between approximately 40 to 60% (bicyclists) and 40 to 70% (motorists) in close range to and smaller at larger distances to CP. For motorists, FPR even increased continuously from approximately 30% (17 m to CP) to 70% (immediately before CP).
-
Underestimation (FNR)—conflicts predicted as non-conflicts— shown as red dashed line, appeared to be less than approximately 20% (bicyclists) and less than 50% (motorists) in closer range to CP and approximately 50 to 90% at larger distances to CP.
Interaction behaviour
Interaction behaviour was analysed by computing pPET for bicyclists along dCP . In Figure 6, pPET is plotted for critical and uncritical encounters. pPET-values smaller than or equal to zero indicate a predicted collision (or road users may have changed their order). For bicyclists, pPET-values of critical encounters differed significantly from uncritical encounters (pPET ≈ 2.1 s, p < .001) within the last 12 m before CP. As expected, at larger distances to CP (i.e. dCP > 12 m) pPET-values were more arbitrary and reached their largest variance between 20 m < dCP < 24 m, but decreased again at even larger distances (i.e. dCP 24 m).
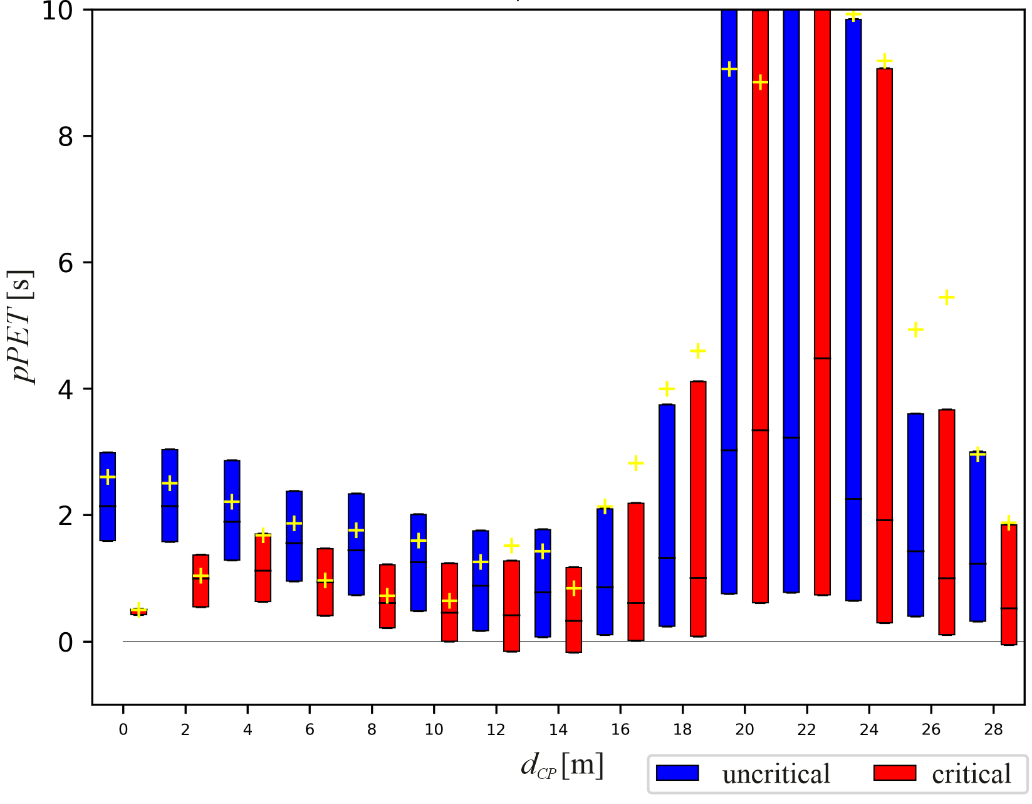
Application of Kruskal-Wallis-H tests on pPET(dCP) supported these findings by the resulting p-values. It revealed significant differences between critical and uncritical situations for motorists up to a distance of 10 m before CP (pmotorists < .05, pbicyclists < .001), and for bicyclists significant differences occurred up to a distance of 26 m before CP (pmotorists = .8, pbicyclists < .05).
Kinematic patterns
Kinematic characteristics of motorists and bicyclists in unaffected, uncritical and critical encounter situations are described by their speeds (Figure 7) and accelerations (Figure 8). Statistical group comparisons were not applied on kinematic data in this study, because they had already been addressed in (Dotzauer et al., 2017). Those results showed significant differences in bicycle speeds and interaction behaviour between critical and uncritical encounter situations (i.e. bicyclists approached with larger speeds), but for motorists, insignificant differences occurred.
Speed
Bicyclists and motorists showed specific patterns in unaffected situations (Figure 7, right). Many motorists stopped at the stop line (i.e. dCP ≈ 30 m) due to red light. After that, approaching the curve, their speeds decreased, which were at minimum of approximately 8 m/s in the centre of the curve. Then, motorists increased their speeds again. Bicyclists continuously decreased their speeds until 2.5 m/s at dCP ≈ 20 m, then accelerated for about 6 m, decelerated until the cyclist crossing at dCP ≈ 4 m and finally crossed the CP accelerating.
In uncritical encounter situations (Figure 7, middle), motorists showed smaller speeds than in unaffected situations in general, which continuously decreased their speeds down to approximately 2 m/s between 4 m ≥ dCP > 2 m and then accelerated again crossing the CP. Bicyclists, however, showed approximately 1 to 2 m/s larger speeds in general than in unaffected situations, particularly if dCP ≤ 12 m (i.e. slightly before curve centre), but the underlying pattern seemed to be similar, particularly at larger distances from the CP.
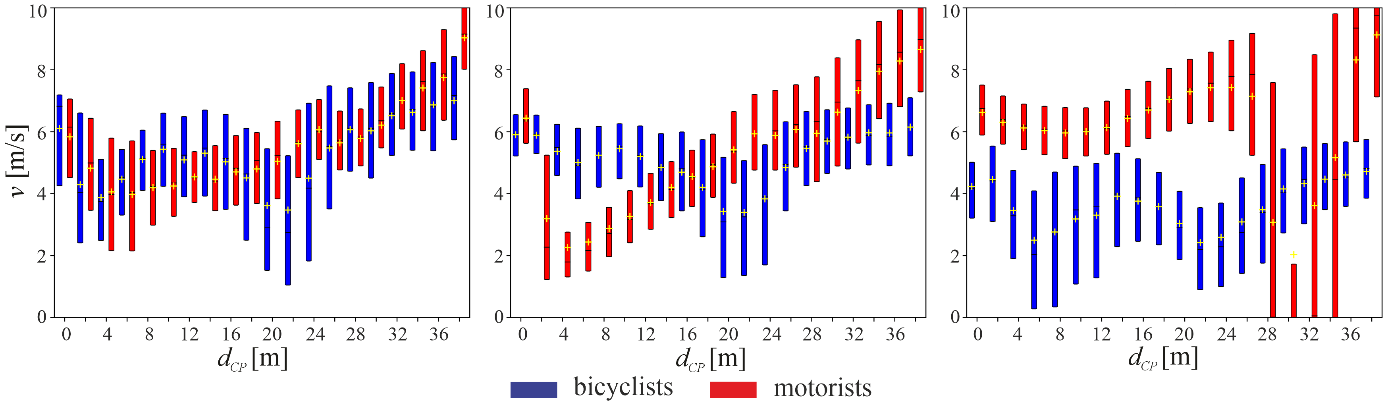
In conflict situations (Figure 7, left), particularly motorists' speeds were larger between 2 to 12 m before CP (i.e. almost within the remaining distance behind the curve centre) in comparison to uncritical encounter situations, whereas the bicyclists' speeds were lower closer to the bicycle crossing and immediately before CP.
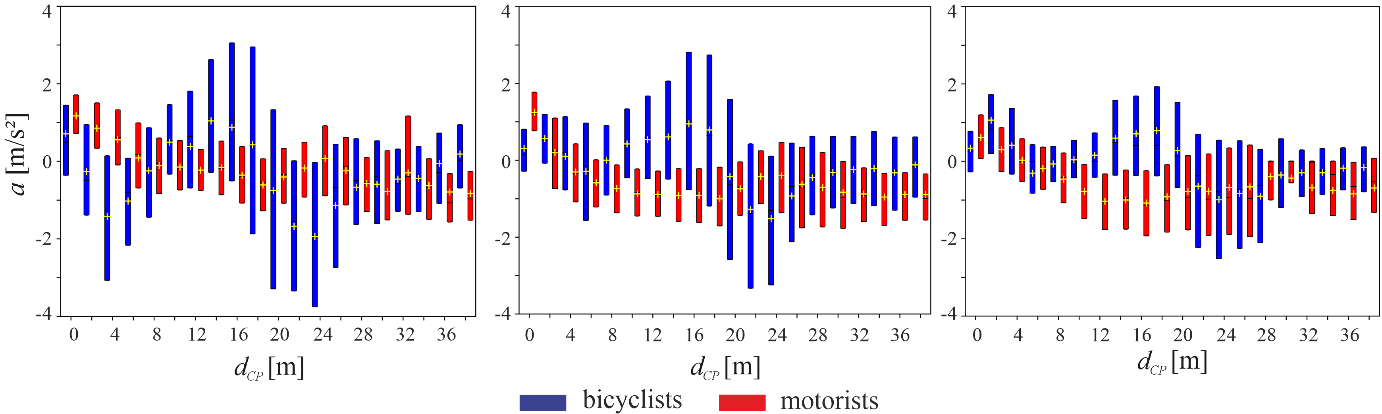
Acceleration
In unaffected situations, motorists and bicyclists approached the intersection quite similarly with accelerations slightly smaller than 0 m/s² until approximately 26 m before CP (Figure 8 , right). The largest differences appeared for bicyclists between 26 m dCP > 10 m (i.e. slightly behind the stop line and before the curve centre). First, bicyclists decelerated between 26 m dCP > 18 m, then accelerated between 18 m dCP > 10 m before CP, and then decelerated again. Immediately before CP, bicyclists accelerated. Motorists, however, almost decelerated all the time, but accelerated again immediately before CP.
In uncritical situations (Figure 8, middle), the patterns of bicyclists and motorists' accelerations in unaffected situations repeat within 18 m dCP > 10 m before CP, although bicyclists' acceleration were larger. In critical situations (Figure 8, left), however, approximately 8 m dCP > 2 m before CP, bicyclists braked intensively, while motorists accelerated. Although large differences in accelerations of bicyclists and motorists in unaffected, uncritical and critical situations appeared, which obviously led to different kinematic and interaction patterns presented above, significant changes appeared in the last meters before CP.
Information theoretic results
On the basis of the results of the interaction behaviour analysed by pPET and the apparent predictability of potentially dangerous situations for bicyclists at approximately 12 m before CP, their manifestation appeared in kinematic patterns and sensitivity exceeding 50% at 12 m before CP (motorists) and 16 m before CP (bicyclists). However, the role of road users' acceleration functions and the question where to reliably warn the road users remained. Therefore, we cut the trajectories dcut {10; 11; 12} m before CP and computed ACFs and CCFs, cross-power spectra, their maxima and entropies and applied inferential statistical tests for the remaining parts.
ACF, CCF and cross-power spectrum
At first, ACFs (bicyclists) and (motorists) (Equation 2) and their mean signal energies (i.e. ) were computed for unaffected, uncritical and critical situations. It appeared (not shown here), that the acceleration functions of motorists were much more correlated than those of bicyclists, because they showed a less steep descent. In case of critical situations not only the descents of bicyclists' ACFs appeared to be steeper than in uncritical and unaffected situations, also their mean signal energies were larger.
Secondly, CCF of bicyclists and motorists and their cross-power density spectra were computed for unaffected, uncritical and critical situations. In Figure 9 the maxima of the CCFs and the cross-power spectra RXY (upper panel) of these situations are presented (only the parts with 0 are shown). Additionally, the idea of quantifying the mean signal energy of ACF was transferred to and RXY to determine their ‘mean cross-signal energy’ and thus, and RXY, max are shown as red stars. Visually, arg max( ) and differed (Figure 9, upper panel). In the cross-power spectra (lower panel) the differences were not that visually distinctive, however, it appeared that these were significant in case dcut {10; 11} m.
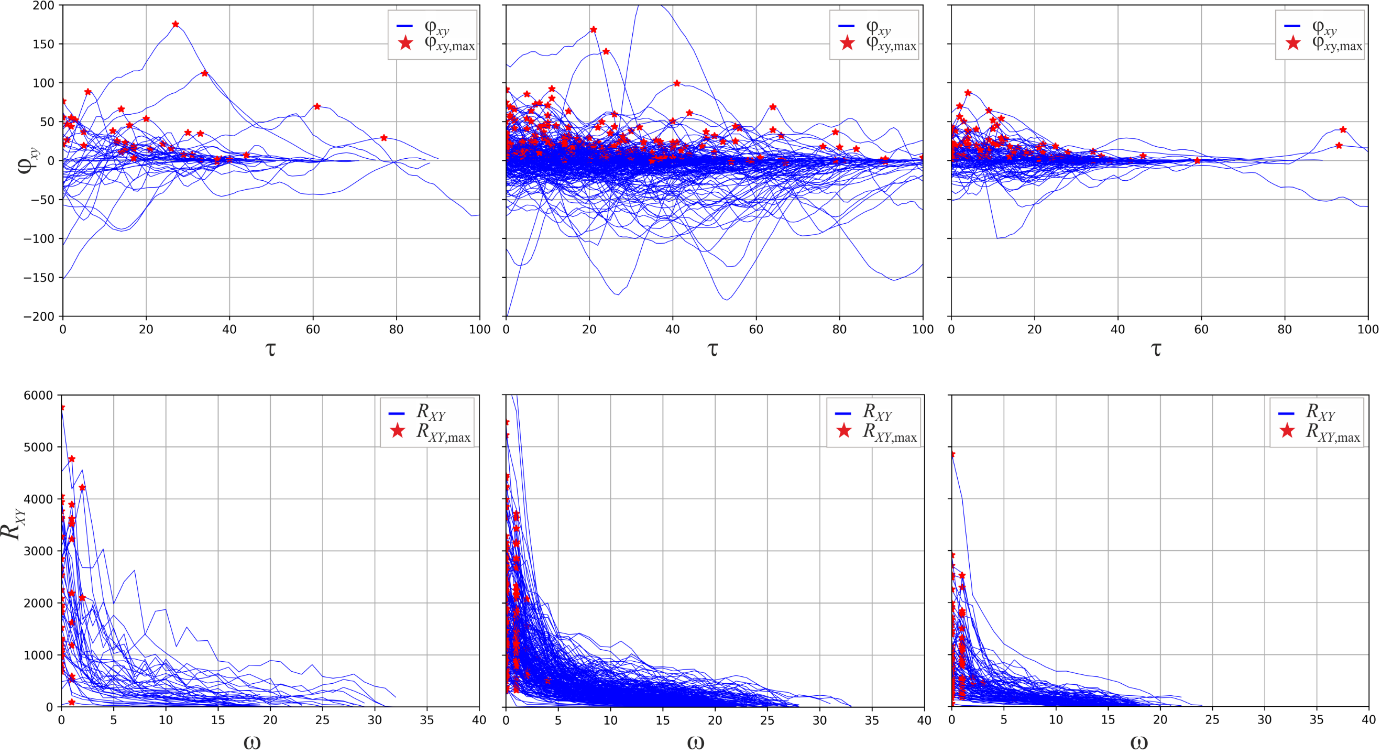
In Figure 10, RXY, max is plotted for critical, uncritical encounters and unaffected situations.
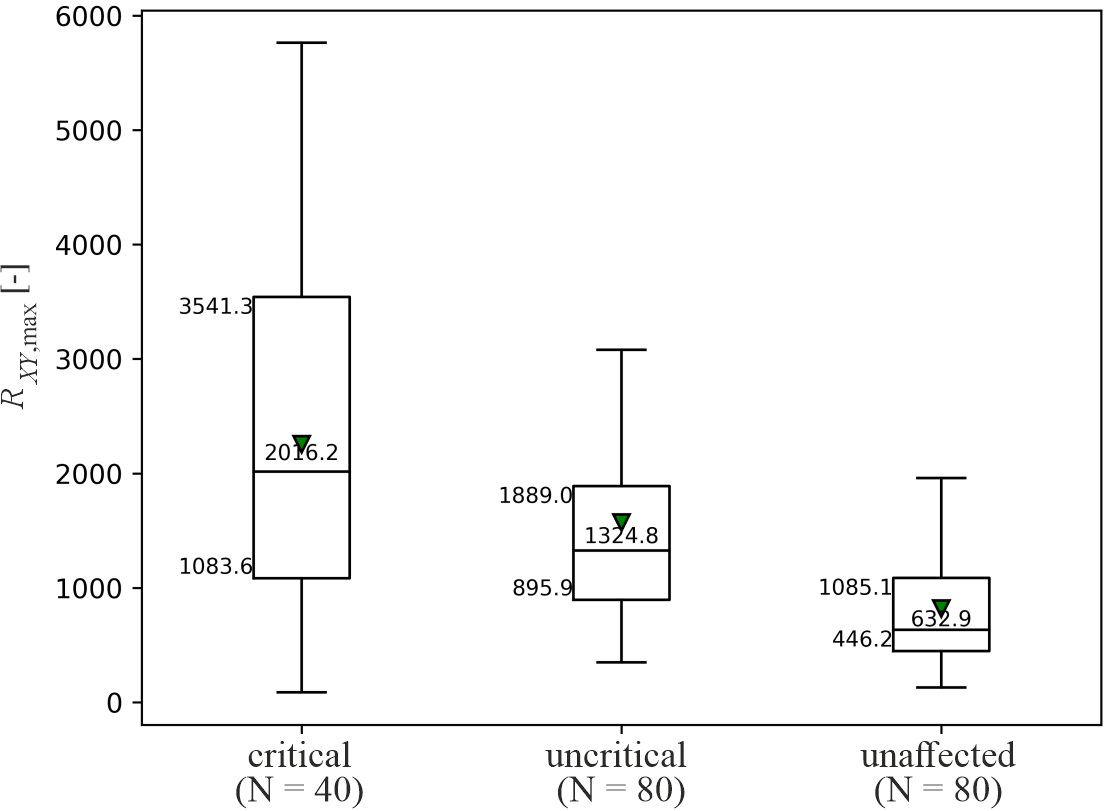
It appeared that the maxima of ‘mean cross-signal energy’ were the largest in case of critical situations, while unaffected situations showed the lowest values. Applying Kruskal-Wallis-H for group comparisons and Mann-Whitney-U tests for single comparisons yielded results as shown in Table 1. The main effect (row ‘C vs U vs N’) showed significant differences among all situations, while the differences between critical and uncritical situations (row ‘C vs U’) appeared to be insignificant for dcut = 12 m. In any other case for dcut the individual comparisons remained significant.
|
Comparison |
dcut = 10 m |
dcut = 11 m |
dcut = 12 m |
|---|---|---|---|
|
C vs U vs N ( = 0.05) |
p < .001 |
p < .001 |
p < .001 |
|
C vs U ( = 0.05/3) |
p = .005 |
p = .016 |
p = .040‡ |
|
C vs N ( = 0.05/3) |
p < .001 |
p < .001 |
p < .001 |
|
U vs N ( = 0.05/3) |
p < .001 |
p < .001 |
p < .001 |
‡ not significant
Entropy
As a consequence of the significant differences between the maxima of the cross-power spectra of critical, uncritical and unaffected situations (section 4.5.1), we computed the entropies of the acceleration functions of bicyclists and motorists likewise. Since entropy differs in case of alphabet binning changes, we tested binnings of 0.5, 1.0 and 2.0 m/s² leading to changes of the maximum entropies, but the underlying patterns remained. Entropy appeared to be robust against binning changes. In Figure 11, entropies of bicyclists' (left half) and motorists' (right half) acceleration functions in critical, uncritical and unaffected situations are presented with ai = 1 m/s² and dcut = 10 m.
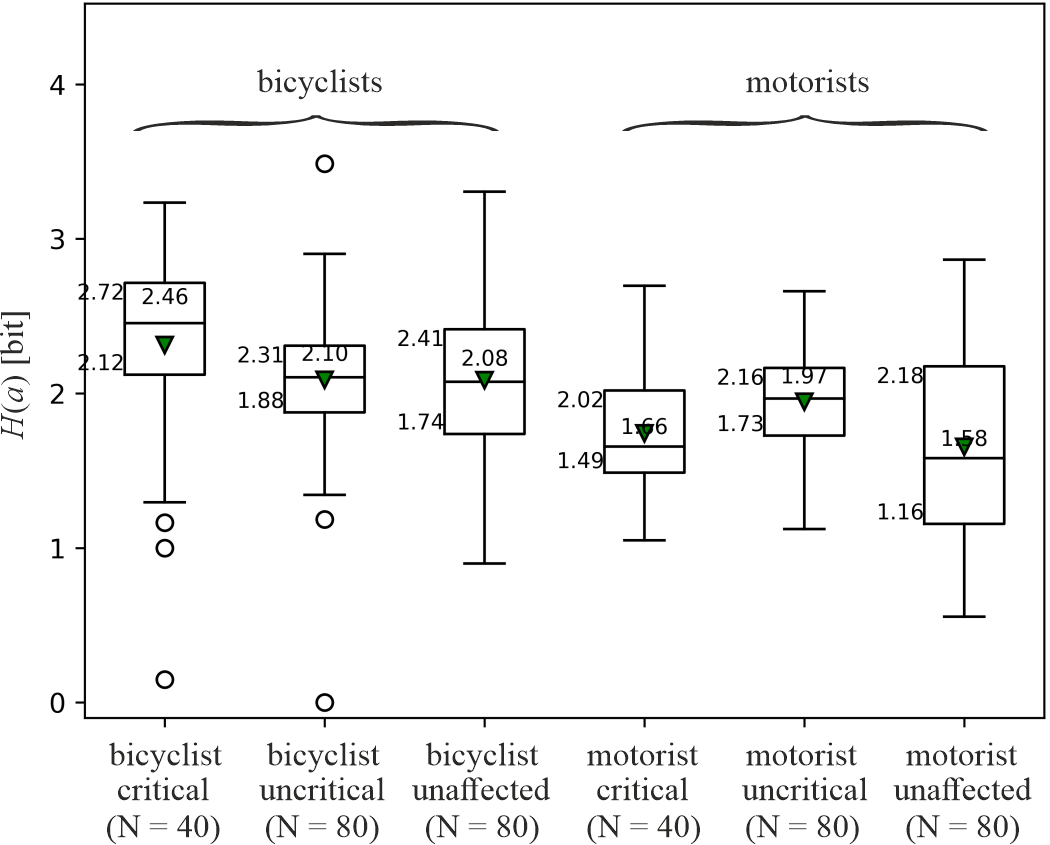
Bicyclists had a significantly larger entropy in case of critical situations (H = 2.46 bit) than in uncritical (H = 2.10 bit) and unaffected situations (H = 2.08 bit). In contrast, motorists had the largest entropy in case of uncritical situations (H = 1.97 bit), whereas their entropies appeared to be smaller in case of critical (H = 1.66 bit) and unaffected situations (H = 1.58 bit). Applying Kruskal-Wallis-H (group comparisons) and Mann-Whitney-U tests (single comparisons) yielded the results shown in Table 2. The main effect (row ‘C vs U vs N’) showed significant differences in general. For bicyclists and motorists, differences between critical and uncritical situations (row ‘C vs U’) as well as for critical and unaffected situations (row ‘C vs N’) appeared to be significant for dcut {10; 11} m, but insignificant for dcut = 12 m. For bicyclists, differences between uncritical and unaffected situations remained insignificant (row ‘U vs N’) for dcut = 10 m. In contrast, for motorists, differences between critical and unaffected situations remained insignificant (row ‘C vs N’) for any dcut .
|
Comparison |
Bicyclists: dcut |
Motorists: dcut |
||||
|---|---|---|---|---|---|---|
|
10 m |
11 m |
12 m |
10 m |
11 m |
12 m |
|
|
C vs U vs N ( = 0.05) |
p = .003 |
p = .002 |
p < .001 |
p < .001 |
p < .001 |
p < .001 |
|
C vs U ( = 0.05/3) |
p < .001 |
p = .009 |
p = .057‡ |
p < .001 |
p < .001 |
p < .001 |
|
C vs N ( = 0.05/3) |
p = .002 |
p < .001 |
p < .001 |
p = .176‡ |
p = .437‡ |
p = .186‡ |
|
U vs N ( = 0.05/3) |
p = .438‡ |
p = .014 |
p < .001 |
p < .001 |
p < .001 |
p < .001 |
‡ not significant
Discussion
The objective of the study was to evaluate a recently developed C-ADAS (Saul et al., 2021) regarding the reliability of a just-in-time warning signal before a potential collision of the interacting right-turning motorists and crossing bicyclists. In this chapter we are discussing the results presented in the previous chapters with regard to decision tree and confusion rates (section 5.1), interaction behaviour (section 5.2), ‘surprise’ or ‘anticipation’ provided by the cross-power spectrum and entropy (section 5.3), and the location of the amber light (section 5.4).
Decision tree and confusion rates
The sensitivity (TPR) and specificity rates (TNR) plotted in Figure 5 clearly show that the amber light, which was triggered by the underlying decision tree, was useful to warn motorists before an upcoming collision in time and not to warn motorists in case of uncritical situations. However, particularly sensitivity values differed for bicyclists (> 50% 16 m before CP) and motorists (> 50% 12 m before CP) in different distances to CP. For motorists, the probabilities of false alarms and non-sent, but required warnings in closer range to CP were larger than for bicyclists. Consequently, predicting potential collisions and non-collisions improved largely below or equal to 12 m before CP, particularly for bicyclists. However, the effect of the amber light on the behaviour of road users was already part of the research in Dotzauer et al. (2018), who showed that the C-ADAS is question made the crossing approximately 11% safer.
Due to the fact that the amount of trajectory data was reduced to situations with PET < 2.5 s, no situations with larger PET-values and consequently, too few trajectory samples were considered for training the decision tree. These are missing uncritical situations (false negatives) and critical ones (false positives), in which the road users had mitigated the conflict before, but ended up with a larger PET due to some relaxation time needed to ‘digest the shock’ (Trullos & Gimm, 2022). As a consequence, a larger annotated training set with more critical and particularly many more uncritical situations would promise to improve reliability of C-ADAS in both cases, which are warning before upcoming collisions and no warning if situations will not develop into conflicts/collisions.
Interaction behaviour and kinematic patterns
The results showed that pPET can be a stable and suitable indicator for predicting conflicts between right-turning motorists and crossing bicyclists already 10 to 11 m before CP; at larger distances to CP their variances increased and thus, predictability decreased. These findings consolidate the results in (Dotzauer et al., 2017), who stated that the last 10 m before meeting at CP make the difference whether an interaction developed into a critical one or not. Depending on the travelled speeds, which are approximately 12 to 23 km/h for motorists and bicyclists within the last 10 m, roughly 1.5 to 2.9 s remain to warn road users before potentially dangerous situations. Clearly, latency times for object detection, trajectory generation and prediction, sending out warnings, etc. at this specific intersection and also road users' reaction times have to be considered too, which decrease this narrow time window further. Actually, we can state that such C-ADAS may not work at large driven speeds at all due to the low time margin available for motorists to perceive warnings and react accordingly. However, as the results of Dotzauer et al. (2018) showed, the application of the amber light resulted in an increase of the PET-values of 11% making this intersection a bit safer. However, the results shown are only valid for the intersection in question and have to be proven for different geometries and topologies. This leads us to the statement that the whole operating mechanism of this specific C-ADAS is not well understood yet.
Reasons for the significant differences in kinematics and pPET-values between motorists and bicyclists in critical and uncritical situations may be, for instance, that motorists mitigated encounter situations from developing to conflicts, because they were aware that bicyclists were present. In fact, in the most cases of uncritical encounter situations, bicyclists were relatively positioned in front of the motorists decreasing their speeds (Dotzauer et al., 2017). However, this is the opposite to critical situations: motorists' characteristics were similar to unaffected situations (i.e. decelerating from entering in the detection area to the middle of the right curve and then accelerating again). A reason for this can be that motorists were not aware of bicyclists riding in their blind spots, yielding kinematics similar to unaffected situations. Bicyclists' kinematic characteristics (particularly the acceleration function), however, showed large differences in the last few meters before CP, which can be interpreted as mitigating conflicts and adapting the situations by strong deceleration. This is also in line with (Dotzauer et al., 2017), in which in case of critical situations, motorists appeared to be more frequent in front of bicyclists (i.e. bicyclists were in their blind spot) and bicyclists tended to cross behind motorists with significantly lower PET. Eventually, we can confirm that the last 10 m before CP make the reliable difference between situations to remain uncritical or to develop into critical ones.
Cross-power spectrum and entropy
The results showed that applying methods of signal processing and information theory on the relevant trajectory data yielded interesting insights in the characteristics of the acceleration functions of right-turning motorists and crossing bicyclists in critical, uncritical and unaffected situations. For instance, it was found that the ‘mean cross-signal energy’ was significantly the largest (also largest variance) in case of critical situations, while unaffected situations showed the lowest values. An interpretation could be that the larger the criticality of an interaction the larger the mean cross-signal energy. This result was also supported by the significant differences of entropies for bicyclists in critical vs uncritical situations if dcut {10; 11} m and—on the other hand—the significant differences of motorists' entropies in uncritical vs critical or unaffected situations. The reasons for this may be—as mentioned earlier—that bicyclists seem to mitigate conflicts to avoid crashes, while motorists seem to avoid uncritical situations to develop into conflicts or crashes. In general, it seems that the comparison between critical (i.e. relevant and dangerous) and uncritical or even unaffected situations leads to reliable results if the last 10 m of the trajectories remained, since the tendency to insignificance increased if dcut increased.
An interesting finding is that bicyclists' entropies appeared to be significantly larger than those of motorists. This can be interpreted by the more uncertain and thus, much less predictable driving behaviour of bicyclists than that of motorists. This, however, seems to be in contrast to the findings by applying pPET and the identified confusion rates. While the pPET-values appeared to be stable for conflict prediction, particularly for bicyclists clearly before 10 m and motorists not before 10 m before CP, sensitivity exceeded 50% for bicyclists already 16 m and for motorists 12 m before CP. This can be explained by the isolated consideration of accelerations functions and by the fact that the decision tree in question (Figure 1, left) did not take accelerations into account, but velocities instead. Further, motorists cannot change their behaviour as sudden as bicyclists can, which should stimulate us to pay more attention on understanding and predicting cycling behaviour, for instance, for designing reliable and accurate (C-) ADAS, particularly for bicyclists.
The question whether we are capable of measuring ‘surprise’ of road users in specific interaction situations cannot be answered in all-encompassing manner. The results showed that we were able to distinguish between critical, uncritical and unaffected situations, particularly in the last 10 m before CP and the differences of driving characteristics between bicyclists and motorists in these situations: motorists avoid interactions to develop into conflicts/collisions by a continuous speed reduction until the bicyclist has passed; and bicyclists mitigate real conflicts by braking immediately before CP. Due to this, we can state that we found a way to measure anticipation of motorists and bicyclists in situations of different criticality.
Location of the amber light before CP
The results suggest the importance of the 0 to 11 m range, however, the installation of an amber light at this position seems not reasonable. The reason for this is that reliable predictions of potentially dangerous situations are available if the interacting road users are 10 to 11 m away from the CP at maximum. Additionally, road users need to have the chance to perceive such an amber light lighting up in time, which already took (latency) time to process the collision risk and transmitting it to the amber light. These are the reasons such an amber light requires an installation much closer to the CP making the challenge of reliably warning interacting road users even more complicated and somehow competing. Eventually, it may happen that such a C-ADAS may not work at all, because the available time for road users after such an amber light lit up is too small to react properly (1.5 to 2.9 s in this research without considering latency times). However, on the one hand, we should think about additional ways to warn the interacting road users, such as directed acoustic warnings. On the other hand, we can increase the amount of available time for road users to get the chance to be warned and act properly. Besides technical ways, such as reduction of latency times, an opportunity, for instance, is to force the motorists to reduce their speeds approaching the intersection, either by infrastructural measures or traffic signs. Another way could be to make the relevant metrics more predictable by harmonising road users speeds at further distances (e.g. 50 m) before the CP. This could lead to more reliable pPET-values, larger sensitivities and specificities and smaller percentages of over- and underestimation at larger distances to CP.
Conclusion and future prospects
The results of this paper show that driving characteristics of bicyclists and motorists differed significantly in critical, uncritical or unaffected situations. Even in case of unaffected situations (i.e. completely undisturbed), specific kinematic patterns appeared for motorists and bicyclists. Essential parameters such as pPET, speed and acceleration, their entropies and maxima of their cross-power spectra, could be identified to assess and even reliably predict spatio-temporal closeness (i.e. conflicts and uncritical encounters) between right-turning motorists and crossing bicyclists already 10 to 11 m before CP. This corresponds to a time horizon of roughly 1.5 to 2.9 s for the road users to perceive collision risk, to get informed and to react and perform evasive actions. This time window reduced further by approximately 0.5 s, since latency times of the whole processing chain (i.e. object detection and classification, trajectory generation, processing and prediction, risk estimation and transmission) could be quantified to average 564 milliseconds at this urban intersection (Manz et al., 2020).
The question posed at the beginning to measure ‘surprise’ cannot be answered, finally, but the results show that we were able to determine anticipation for bicyclists in critical and for motorists in uncritical situations. It was found that the acceleration functions of road users have a significant value, particularly up to 10 m before CP, for designing C-ADAS. However, they should not be considered isolated, but, as a joint metric together with pPET instead.
This research showed that installation, operation and reliable effect of C-ADAS on road user safety (particularly cycling safety) are complex and sophisticated. On the one hand, we obtained reliable results—as shown above—10 m before CP, which corresponds to roughly 1 to 2.4 s road users' available reaction time. But according to Green (2000), mean reaction times in case of unexpected or even surprised braking situations appeared to be approximately 1.25 s or 1.5 s, respectively. Consequently, this C-ADAS in question may not be able to warn all relevant road users before potentially dangerous situations. Therefore, this small amount of time could be increased by infrastructural (e.g. increase the curvature) or operational (e.g. traffic signs or speed control) measures to decrease and/or harmonise speeds of interacting road users at further distances to CP. However, as Dotzauer et al. (2018) showed, this specific amber light made this intersection approximately 11% safer without any of these measures mentioned. This leads the point to state that the mechanism of this C-ADAS is still not completely understood and needs to be studied further. This includes the definition and quantification of the competing requirements, such as amber light visibility, additional warning measures (e.g. acoustic warnings), robustness and reliability of collision prediction, early warnings of the interacting road users, decrease of latency and reaction times, relevant and suitable metrics and acceptance. This requires a thorough examination of the intersection regarding geometry, topology, traffic relations and control as well as the kinematic and conflict-related parameters of the interacting road users. These results do not only help to design future C-ADAS in order to warn motorists before potential conflicts/collisions, they are the basis for developing cycling assistance systems, which also means to transfer sensors, technologies and algorithms to the bicycle.
Our future work will deal with trying to better understand the effective mechanism of this specific C-ADAS. This includes examining different types of crossings, geometries and topologies, critical, uncritical and also unaffected situations and integrating the findings concerning the motorists' and bicyclists' behavioural patterns, particularly their acceleration functions, in a novel method for trajectory and collision/conflict prediction. Additionally, we found the maxima of the cross-power spectra significantly differing depending of the criticality of the interaction, which is not completely understood. We will improve the current infrastructure-based processing chain to receive more accurate trajectories (particularly for bicyclists and pedestrians), extend our data base with more critical and uncritical situations and try to get a more detailed insight to measure ‘surprise’ in traffic by, for instance, designing a joint entropy that involves acceleration and pPET as some sort of combination metric. Furthermore, we think, a more comprehensive approach is necessary that takes the situation awareness of the interaction partners into account. Therefore, we aim to conduct eye-tracking studies and equip bicyclists and motorists to quantify situation awareness of them in such situations.
Declaration of competing interests
The authors report no competing interests.
Availability of data
The data are available on request to the authors.
Funding
This work received funding from German Federal Ministry for Digital and Transport (BMDV), research grant 45AVF2010E.
CRediT contribution statement
Marek Junghans: Conceptualization, Formal analysis, Funding acquisition, Methodology, Project administration, Software, Supervision, Visualization, Writing—original draft.
Meng Zhang: Data curation, Resources, Software, Validation, Writing—review & editing.
Hagen Saul: Conceptualization, Data curation, Resources, Software, Validation, Writing—review & editing.
Andreas Leich: Conceptualization, Writing—review & editing.